Hypothesis Testing: Summarizing Information about Causal Effects
Fill In Your Name
01 March 2022
- The Role of Hypothesis Tests in Causal Inference
- Hypothesis Testing Basics
- Ingredients of a hypothesis test
- A hypothesis is a statement about or model of a relationship between potential outcomes
- Test statistics summarize treatment-to-outcome relationships
- The design links test statistic and hypothesis
- The design guides creation of a distribution of hypothetical test statistics
- Plot the randomization distributions under the null
- \(p\)-values summarize the plots
- How to do this in R: COIN
- How to do this in R: RItools
- How to do this in R: RI2
- Next topics
- Testing weak null hypotheses
- Rejecting null hypotheses
- Rejecting hypotheses and making errors
- False positive rates in hypothesis testing
- False positive and false negative errors
- A single test of a single hypothesis
- Decisions imply errors
- Diagnosing false positive rates by simulation
- Diagnosing false positive rates by simulation
- Diagnosing false positive rates by simulation
- Diagnosing false positive rates by simulation
- Diagnosing false positive rates by simulation
- False positive rate with \(N=60\) and binary outcome
- False positive rate with \(N=60\) and continuous outcome
- Summary
- Advanced Topics
- Testing many hypotheses
- When might we test many hypotheses?
- False positive rates in multiple hypothesis testing
- Discoveries with multiple tests
- Two main error rates to control when testing many hypotheses
- Questions with multiple outcomes
- Multiple hypothesis testing: Multiple Outcomes
- Can we detect an
effect on outcome
Y1? - On which of the five outcomes can we detect an effect?
- Can we detect an effect for any of the five outcomes?
- Comparing approaches I
- Comparing approaches II
- The Holm correction
- Multiple hypothesis testing: Multiple treatment arms
- Multiple hypothesis testing: Multiple treatment arms
- Multiple hypothesis testing: Multiple treatment arms
- Approaches to testing hypotheses with multiple arms
- Summary
- References
The Role of Hypothesis Tests in Causal Inference
Key points for this lecture
Statistical inference (e.g., hypothesis tests and confidence intervals) requires inference — reasoning about the unobserved.
\(p\)-values require probability distributions.
Randomization (or Design) + a Hypothesis + a Test Statistic Function \(\rightarrow\) probability distributions representing the hypothesis (reference distributions)
Observed Values of Test Statistics + Reference Distribution \(\rightarrow\) \(p\)-value.
The role of hypothesis tests in causal inference I
The fundamental problem of causal inference says that we can see only one potential outcome for any given unit.
So, if a counterfactual causal effect of the treatment, \(T\), for Jake occurs when \(y_{\text{Jake},T=1} \ne y_{\text{Jake},T=0}\), then how can we learn about the causal effect?
One solution is the estimation of averages of causal effects (the ATE, ITT, LATE).
This is what we call Neyman’s approach.
The role of hypothesis tests in causal inference II
Another solution is to make claims or guesses about the causal effects.
We could say, “I think that the effect on Jake is 5.” or “This experiment had no effect on anyone.” And then we ask “How much evidence does this experiment have about that claim?”
This evidence is summarized in a \(p\)-value.
We call this Fisher’s approach.
The role of hypothesis tests in causal inference III
The hypothesis testing approach to causal inference doesn’t provide a best guess but instead tells you how much evidence or information the research design provides about a causal claim.
The estimation approach provides a best guess but doesn’t tell you how much you know about that guess.
- For example, a best guess with \(N=10\) seems to tell us less about the effect than \(N=1000\).
- For example, a best guess when 95% of \(Y=1\) and 5% of \(Y=0\) seems to tell us less than when outcomes are evenly split betwee 0 and 1.
We nearly always report both since both help us make decisions: “Our best guess of the treatment effect was 5, and we could reject the idea that the effect was 0 (\(p\)=.01).”
Hypothesis Testing Basics
Ingredients of a hypothesis test
A hypothesis is a statement about a relationship among potential outcomes.
A test statistic summarizes the relationship between treatment and observed outcomes.
The design allows us to link the hypothesis and the test statistic: calculate a test statistic that describes a relationship between potential outcomes.
The design also tells us how to generate a distribution of possible test statistics implied by the hypothesis.
A \(p\)-value describes the relationship between our observed test statistic and the distribution of possible hypothesized test statistics.
A hypothesis is a statement about or model of a relationship between potential outcomes
| Outcome | Treatment | \(y_{i,0}\) | ITE | \(y_{i,1}\) | \(Y>0\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 10 | 10 | 0 |
| 30 | 1 | 0 | 30 | 30 | 0 |
| 0 | 0 | 0 | 200 | 200 | 0 |
| 1 | 0 | 1 | 90 | 91 | 0 |
| 11 | 1 | 1 | 10 | 11 | 0 |
| 23 | 1 | 3 | 20 | 23 | 0 |
| 34 | 1 | 4 | 30 | 34 | 0 |
| 45 | 1 | 5 | 40 | 45 | 0 |
| 190 | 0 | 190 | 90 | 280 | 1 |
| 200 | 0 | 200 | 20 | 220 | 1 |
For example, the sharp, or strong, null hypothesis of no effects is \(H_0: y_{i,1} = y_{i,0}\)
Test statistics summarize treatment-to-outcome relationships
## The mean difference test statistic
meanTT <- function(ys, z) {
mean(ys[z == 1]) - mean(ys[z == 0])
}
## The difference of mean ranks test statistic
meanrankTT <- function(ys, z) {
ranky <- rank(ys)
mean(ranky[z == 1]) - mean(ranky[z == 0])
}
observedMeanTT <- meanTT(ys = Y, z = T)
observedMeanRankTT <- meanrankTT(ys = Y, z = T)
observedMeanTT[1] -49.6[1] 1The design links test statistic and hypothesis
What we observe for each person \(i\) (\(Y_i\)) is either what we would have observed in treatment (\(y_{i,1}\)) or what we would have observed in control (\(y_{i,0}\)).
\[Y_i = T_i y_{i,1} + (1-T_i)* y_{i,0}\]
So, if \(y_{i,1}=y_{i,0}\) then \(Y_i = y_{i,0}\).
What we actually observe is what we would have observed in the control condition.
The design guides creation of a distribution of hypothetical test statistics
We need to know how to repeat our experiment:
Then we repeat it, calculating the implied test statistic by the hypothesis and design each time:
Plot the randomization distributions under the null
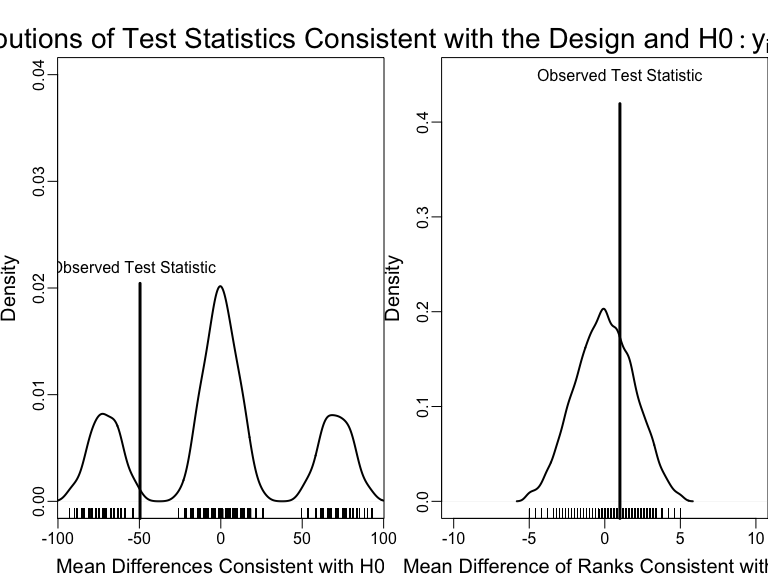
An example of using the design of the experiment to test a hypothesis with two different test statistics.
\(p\)-values summarize the plots
How should we interpret these \(p\)-values? (Notice that they are one-tailed.)
pMeanTT <- mean(possibleMeanDiffsH0 >= observedMeanTT)
pMeanRankTT <- mean(possibleMeanRankDiffsH0 >= observedMeanRankTT)
pMeanTT[1] 0.7785[1] 0.3198How to do this in R: COIN
## using the coin package
library(coin)
set.seed(12345)
pMean2 <- coin::pvalue(oneway_test(Y ~ factor(T),
data = dat,
distribution = approximate(nresample = 1000), alternative = "less"
))
dat$rankY <- rank(dat$Y)
pMeanRank2 <- coin::pvalue(oneway_test(rankY ~ factor(T),
data = dat,
distribution = approximate(nresample = 1000), alternative = "less"
))
pMean2[1] 0.783
99 percent confidence interval:
0.7476 0.8157 [1] 0.323
99 percent confidence interval:
0.2853 0.3624 How to do this in R: RItools
First install a development version of the RItools package
# dev_mode() ## dont install the package globally
renv::install("markmfredrickson/RItools@randomization-distribution",
force = TRUE
)
# dev_mode()Then use the RItest function.
# dev_mode()
library(RItools)
thedesignA <- simpleRandomSampler(total = N, z = dat$T, b = rep(1, N))
pMean4 <- RItest(
y = dat$Y, z = dat$T, samples = 1000, test.stat = meanTT,
sampler = thedesignA
)
pMeanRank4 <- RItest(
y = dat$Y, z = dat$T, samples = 1000, test.stat = meanrankTT,
sampler = thedesignA
)
pMean4
pMeanRank4
# dev_mode() ## and turn off dev_modeHow to do this in R: RI2
How should we interpret the two-tailed \(p\)-value here?
## using the ri2 package
library(ri2)
thedesign <- declare_ra(N = N)
dat$Z <- dat$T
pMean4 <- conduct_ri(Y ~ Z,
declaration = thedesign,
sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMean4) term estimate two_tailed_p_value
1 Z -49.6 0.4444pMeanRank4 <- conduct_ri(rankY ~ Z,
declaration = thedesign,
sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMeanRank4) term estimate two_tailed_p_value
1 Z 1 0.6349Next topics
Testing weak null hypotheses, \(H_0: \bar{y}_{1} = \bar{y}_{0}\).
Rejecting null hypotheses (and making false positive and/or false negative errors).
Maintaining correct false positive error rates when testing more than one hypothesis.
Power of hypothesis tests (Module on Statistical Power and Design Diagnosands).
Testing weak null hypotheses
Testing the weak null of no average effects
The weak null hypothesis is a claim about aggregates, and it is nearly always stated in terms of averages: \(H_0: \bar{y}_{1} = \bar{y}_{0}\)
The test statistic for this hypothesis is nearly always the simple difference of means (i.e.,
meanTT()above).
lm1 <- lm(Y ~ T, data = dat)
lm1P <- summary(lm1)$coef["T", "Pr(>|t|)"]
ttestP1 <- t.test(Y ~ T, data = dat)$p.value
library(estimatr)
ttestP2 <- difference_in_means(Y ~ T, data = dat)
c(lm1P = lm1P, ttestP1 = ttestP1, tttestP2 = ttestP2$p.value) lm1P ttestP1 tttestP2.T
0.3321 0.3587 0.3587 - Why is the OLS \(p\)-value different? What assumptions do we use to calculate it?
Testing the weak null of no average effects
Both variation and location of \(Y\) changes with treatment in this simulation.
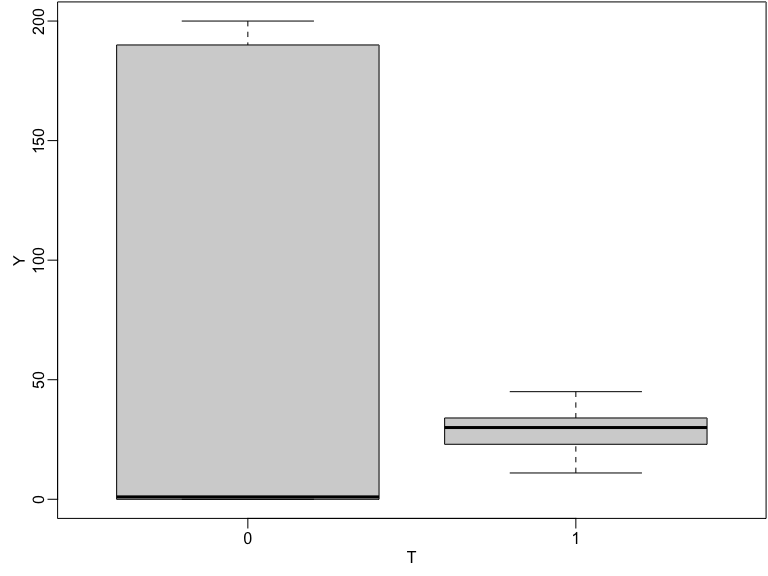
Boxplot of observed outcomes by treatment status
Testing the weak null of no average effects
## By hand:
varEstATE <- function(Y, T) {
var(Y[T == 1]) / sum(T) + var(Y[T == 0]) / sum(1 - T)
}
seEstATE <- sqrt(varEstATE(dat$Y, dat$T))
obsTStat <- observedMeanTT / seEstATE
c(
observedTestStat = observedMeanTT,
stderror = seEstATE,
tstat = obsTStat,
pval = 2 * min(
pt(obsTStat, df = 8, lower.tail = TRUE),
pt(obsTStat, df = 8, lower.tail = FALSE)
)
)observedTestStat stderror tstat pval
-49.6000 48.0448 -1.0324 0.3321 Rejecting null hypotheses
Rejecting hypotheses and making errors
“In typical use, the level of the test [\(\alpha\)] is a promise about the test’s performance and the size is a fact about its performance…” (Rosenbaum 2010, Glossary)
\(\alpha\) is the probability of rejecting the null hypothesis when the null hypothesis is true.
How should we interpret \(p\)=0.78? What about \(p\)=0.32 (our tests of the sharp null)?
What does it mean to “reject” \(H_0: y_{i,1}=y_{i,2}\) at \(\alpha=.05\)?
False positive rates in hypothesis testing
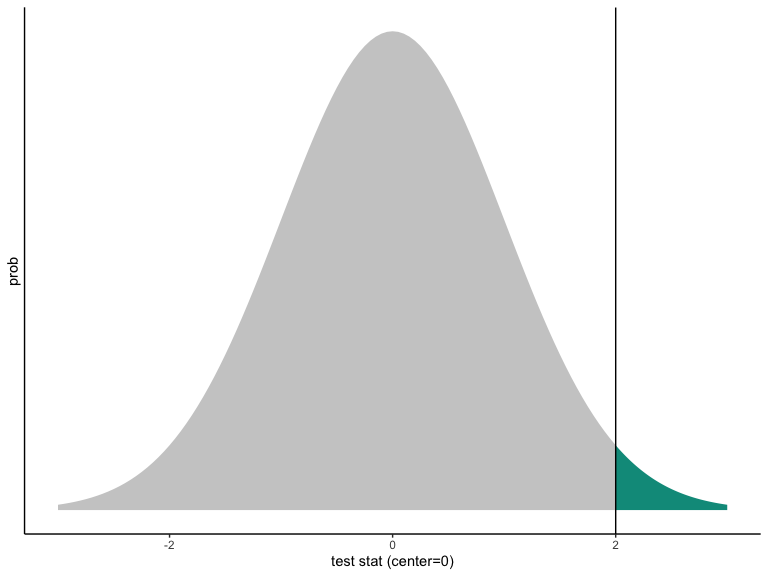
One-sided p-value from a Normally distributed test statistic.
Notice:
The curve is centered at the hypothesized value.
The curve represents the world of the hypothesis.
The \(p\)-value is how rare it would be to see the observed test statistic (or a value farther away from the hypothesized value) in the world of the null.
In the picture, the observed value of the test statistic is consistent with the hypothesized distribution, but just not super consistent.
Even if \(p < .05\) (or \(p < .001\)) the observed test statistic must reflect some value on the hypothesized distribution. This means that you can always make an error when you reject a null hypothesis.
False positive and false negative errors
If we say, “The experimental result is significantly different from the hypothesized value of zero (\(p=.001\))! We reject that hypothesis!” when the truth is zero we are making a false positive error (claiming to detect something positively when there is no signal, only noise).
If we say, “We cannot distinguish this result from zero (\(p=.3\)). We cannot reject the hypothesis of zero.” when the truth is not zero we are making a false negative error (claiming inability to detect something when there is a signal, but it is overwhelmed by noise.)
A single test of a single hypothesis
A single test of a single hypothesis should encourage false positive errors rarely (for example, if we set \(\alpha=.05\)) then we are saying that we are comfortable with our testing procedure making false positive errors in no more than 5% of tests of a given treatment assignment in a given experiment.
Also, a single test of a single hypothesis should detect signal when it exists — it should be have high statistical power. In other words, it should not fail to detect a signal when it exists (i.e. should have low false negative error rates).
Decisions imply errors
If errors are necessary, how can we diagnose them? How do we learn whether our hypothesis-testing procedure might generate too many false positive errors?
Diagnose by simulation!
Diagnosing false positive rates by simulation
Across repetitions of the design:
- Create a true null hypothesis.
- Test the true null.
- The \(p\)-value should be large if the test is operating correctly.
The proportion of small \(p\)-values should be no larger than \(\alpha\) if the test is operating correctly.
Diagnosing false positive rates by simulation
Example with a binary outcome. Does the test work as it should? What do the p-values look like when there is no effect?
collectPValues <- function(y, trt, thedistribution = exact()) {
## Make Y and T have no relationship by re-randomizing T
new_trt <- repeatExperiment(length(y))
thedata <- data.frame(new_trt = new_trt, y = y)
thedata$ranky <- rank(y)
thedata$new_trtF <- factor(thedata$new_trt)
## The four tests
thelm <- lm(y ~ new_trt, data = thedata)
t_test_CLT <- difference_in_means(y ~ new_trt, data = thedata)
t_test_exact <- oneway_test(y ~ new_trtF,
data = thedata,
distribution = thedistribution
)
t_test_rank_exact <- oneway_test(ranky ~ new_trtF,
data = thedata,
distribution = thedistribution
)
owP <- coin::pvalue(t_test_exact)[[1]]
owRankP <- coin::pvalue(t_test_rank_exact)[[1]]
## Return the p-values
return(c(
lmp = summary(thelm)$coef["new_trt", "Pr(>|t|)"],
neyp = t_test_CLT$p.value[[1]],
rtp = owP,
rtpRank = owRankP
))
}Diagnosing false positive rates by simulation
When there is no effect, a test of the null hypothesis of no effects should produce a big p-value.
If the test is working well, we should see mostly big p-values and very few small p-values.
A few of the p-values for the four different tests (we did 5000 simulations, just showing 5)
[,1] [,2] [,3] [,4] [,5]
lmp 1 1 1 1 0.1411
neyp 1 1 1 1 0.1778
rtp 1 1 1 1 0.4444
rtpRank 1 1 1 1 0.4444Diagnosing false positive rates by simulation
In fact, if there is no effect, and if we decided to reject the null hypothesis of no effects with \(\alpha=.25\), we would want no more than 25% of our p-values in this simulation to be less than p=.25. What do we see here? Which tests appear to have false positive rates that are too high?
## Calculate the proportion of p-values less than .25 for each row of pDist
apply(pDist, 1, function(x) {
mean(x < .25)
}) lmp neyp rtp rtpRank
0.4536 0.4536 0.0000 0.0000 Diagnosing false positive rates by simulation
Compare tests by plotting the proportion of p-values less than any given number. The “randomization inference” tests control the false positive rate (these are the tests of using direct permutation, repeating the experiment).
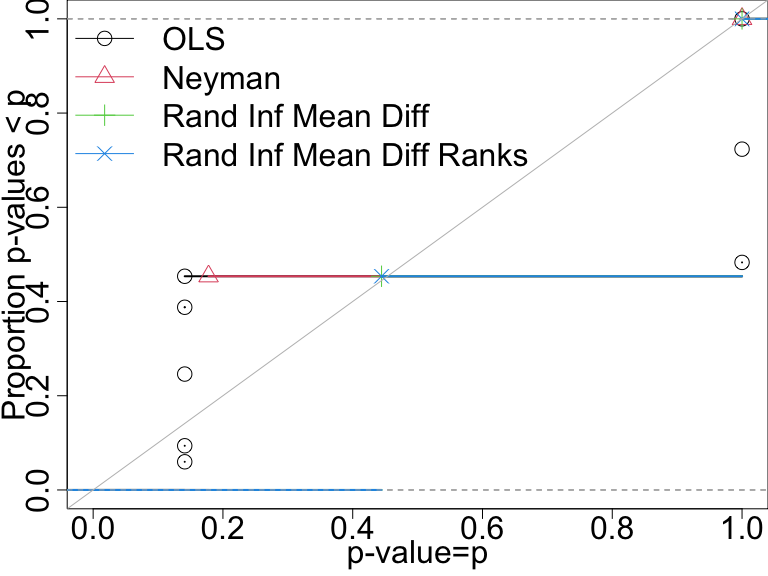
P-value distributions when there are no effects for four tests with n=10. A test that controls its false positive rate should have points on or below the diagonal line.
False positive rate with \(N=60\) and binary outcome
In this design only the direct randomization inference-based tests control the false positive rate.
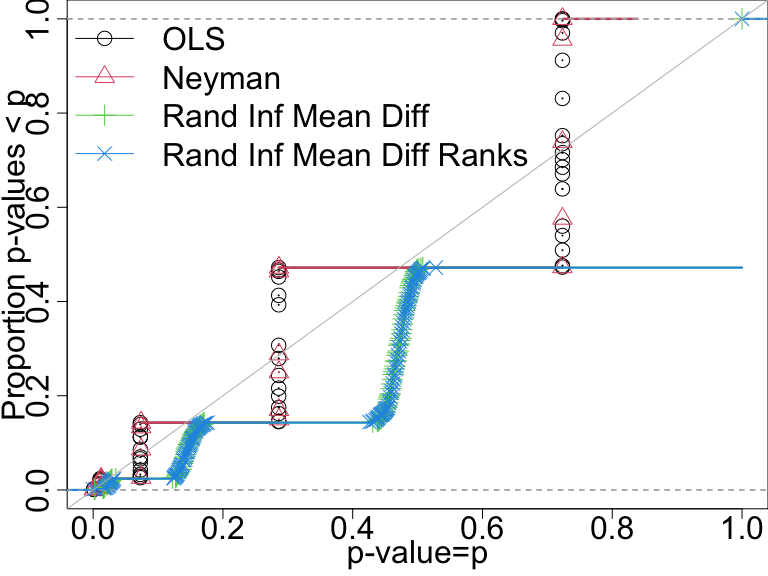
P-value distributions when there are no effects for four tests with n=60 and a binary outcome. A test that controls its false positive rate should have points on or below the diagonal line.
False positive rate with \(N=60\) and continuous outcome
Here, all of the tests do a good job of controlling the false positive rate.
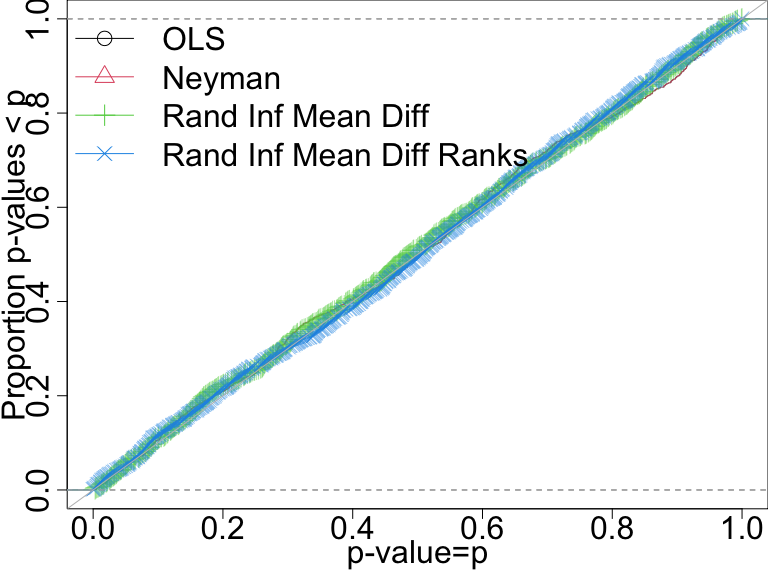
P-value distributions when there are no effects for four tests with n=60 and a continuous outcome. A test that controls its false positive rate should have points on or below the diagonal line.
Summary
A good test:
casts doubt on the truth rarely, and
easily distinguishes signal from noise (casts doubt on falsehoods often).
We can learn whether our testing procedure controls false positive rates given our design.
When false positive rates are not controlled, what might be going wrong? (Often has to do with asymptotics.)
Advanced Topics
Some advanced topics connected to hypothesis testing
Even if a given testing procedure controls the false positive rate for a single test, it may not control the rate for a group of multiple tests. See 10 Things you need to know about multiple comparisons for a guide to the approaches to controlling such rejection-rates in multiple tests.
A \(100(1-\alpha)\)% confidence interval can be defined as the range of hypotheses where all of the \(p\)-values are greater than or equal to \(\alpha\). This is called inverting the hypothesis test (Rosenbaum (2010)). That is, a confidence interval is a collection of hypothesis tests.
What else to know about hypothesis tests
A point estimate based on hypothesis testing is called a Hodges-Lehmann point estimate (Rosenbaum (1993),Hodges and Lehmann (1963)).
A set of hypothesis tests can be combined into one single hypothesis test (Hansen and Bowers (2008),Caughey, Dafoe, and Seawright (2017)).
In equivalence testing, one can hypothesize that two test-statistics are equivalent (i.e., the treatment group is the same as the control group) rather than only about one test-statistic (the difference between the two groups is zero) (Hartman and Hidalgo (2018)).
Since a hypothesis test is a model of potential outcomes, one can use hypothesis testing to learn about complex models, such as models of spillover and propagation of treatment effects across networks (Bowers, Fredrickson, and Panagopoulos (2013), Bowers, Fredrickson, and Aronow (2016), Bowers et al. (2018))
Exercise: Hypothesis Tests and Test Statistics
If an intervention was very effective at increasing the variability of an outcome but did not change the mean, would the \(p\)-value reported by R or Stata if we used
lm_robust()ordifference_of_means()orregort.testbe large or small?If an intervention caused the mean in the control group to be moderately reduced but increased a few outcomes a lot (like a 10 times effect), would the \(p\)-value from R
lm_robust()ordifference_of_means()be large or small?
Testing many hypotheses
When might we test many hypotheses?
Does the effect of an experimental treatment differ between different groups? Could differences in treatment effect arise because of some background characteristics of experimental subjects?
Which, among several, strategies for communication were most effective on a single outcome?
Which, among several outcomes, were influenced by a single experimental intervention?
False positive rates in multiple hypothesis testing
Say our probability of making a false positive error is .05 in a single test. What happens if we ask: (1) which of these 10 outcomes has a statistically significant relationship with the two arms of treatment? or (2) which of these 10 treatment arms had a statistically significant relationship with the single outcome?
- Prob of false positive error should be less than or equal to .05 in 1 test.
- Prob of one false positive error should be less than or equal to \(1 - ( ( 1 - .05 ) \times (1 - .05) ) = .0975\) in 2 tests.
- Prob of at least one false positive error with \(\alpha=.05\) in 10 tests should be \(\le\) \(1 - (1-.05)^{10}=.40\).
Discoveries with multiple tests
Number of errors committed when testing \(m\) null hypotheses (Benjamini and Hochberg 1995 ’s Table 1). Cells are numbers of tests. \(R\) is # of “discoveries” and \(V\) is # of false discoveries, \(U\) is # of correct non-rejections, and \(S\) is # of correct rejections.
| Declared Non-Significant | Declared Significant | Total | |
|---|---|---|---|
| True null hypotheses (\(H_{true}=0\)) | |
|
\(m_0\) |
| Not true null hyps (\(H_{true} \ne 0\)) | |
|
m - \(m_0\) |
| Total | |
|
m |
Two main error rates to control when testing many hypotheses
Family wise error rate (FWER) is \(P(V>0)\) (Probability of any false positive error).
We’d like to control this if we plan to make a decision about the results of our multiple tests. The research project is mostly confirmatory.
See, for example, the projects of the OES https://oes.gsa.gov: federal agencies will make decisions about programs depending on whether they detect results or not.
False Discovery Rate (FDR) is \(E(V/R | R>0)\) (Average proportion of false positive errors given some rejections).
We’d like to control this if we are using this experiment to plan the next experiment. We are willing to accept a higher probability of error in the interests of giving us more possibilities for discovery.
For example, one could imagine an organization, a government, an NGO, could decide to conduct a series of experiments as a part of a learning agenda: no single experiment determines decision making, more room for exploration.
We will focus on FWER but recommend thinking about FDR and learning agendas as a very useful way to go.
Questions with multiple outcomes
What is the effect of one treatment on multiple outcomes?
On which outcomes (out of many) did the treatment have an effect?
The second question, in particular, can lead to the kind of uncontrolled family wise error rate problems that we referred to above.
Multiple hypothesis testing: Multiple Outcomes
Imagine we had five outcomes and one treatment (showing potential and observed outcomes here):
ID T Y1_T_0 Y1_T_1 Y2_T_0 Y2_T_1 Y3_T_0 Y3_T_1 Y4_T_0 Y4_T_1 Y5_T_0 Y5_T_1
1 001 0 0.19 0.19 0.366 0.366 0.546 0.546 -0.626 -0.626 -0.125 -0.125
2 002 0 -0.43 -0.43 0.931 0.931 -2.233 -2.233 1.309 1.309 1.078 1.078
3 003 0 0.91 0.91 -1.907 -1.907 0.288 0.288 -0.133 -0.133 -1.261 -1.261
4 004 0 1.79 1.79 0.052 0.052 0.544 0.544 -1.608 -1.608 -0.452 -0.452
5 005 1 1.00 1.00 -0.848 -0.848 -1.192 -1.192 -1.308 -1.308 -1.027 -1.027
6 006 0 1.11 1.11 -0.368 -0.368 -0.018 -0.018 -0.045 -0.045 0.068 0.068 ID T Y1 Y2 Y3 Y4 Y5
1 001 0 0.19 0.366 0.546 -0.626 -0.125
2 002 0 -0.43 0.931 -2.233 1.309 1.078
3 003 0 0.91 -1.907 0.288 -0.133 -1.261
4 004 0 1.79 0.052 0.544 -1.608 -0.452
5 005 1 1.00 -0.848 -1.192 -1.308 -1.027
6 006 0 1.11 -0.368 -0.018 -0.045 0.068Can we detect an effect on outcome Y1?
Can we detect an effect on outcome Y1? (i.e., does the
hypothesis test produce a small enough \(p\)-value?)
[1] 0.88## Notice that the t-test p-value is also a chi-squared test
## p-value.
coin::pvalue(independence_test(Y1 ~ factor(T),
data = dat1,
teststat = "quadratic"
))[1] 0.88On which of the five outcomes can we detect an effect?
On which of the five outcomes can we detect an effect? (i.e., does any of the five hypothesis tests produce a small enough \(p\)-value?)
p1 <- coin::pvalue(oneway_test(Y1 ~ factor(T), data = dat1))
p2 <- coin::pvalue(oneway_test(Y2 ~ factor(T), data = dat1))
p3 <- coin::pvalue(oneway_test(Y3 ~ factor(T), data = dat1))
p4 <- coin::pvalue(oneway_test(Y4 ~ factor(T), data = dat1))
p5 <- coin::pvalue(oneway_test(Y5 ~ factor(T), data = dat1))
theps <- c(p1 = p1, p2 = p2, p3 = p3, p4 = p4, p5 = p5)
sort(theps) p5 p4 p3 p2 p1
0.27 0.30 0.43 0.59 0.88 Can we detect an effect for any of the five outcomes?
Can we detect an effect for any of the five outcomes? (i.e., does the hypothesis test for all five outcomes at once produce a small enough \(p\)-value?)
coin::pvalue(independence_test(Y1 + Y2 + Y3 + Y4 + Y5 ~ factor(T),
data = dat1, teststat = "quadratic"
))[1] 0.67Which approach is likely to mislead us with too many “statistically significant” results (5 tests or 1 omnibus test)?
Comparing approaches I
Let’s do a simulation to learn about these testing approaches.
We will (1) set the true causal effects to be 0, (2) repeatedly re-assign treatment, and (3) each time, do each of those three tests.
Since the true effect is 0, we expect most of the \(p\)-values to be large. (In fact, we’d like no more than 5% of the \(p\)-values to be greater than \(p=.05\) if we are using the \(\alpha=.05\) accept-reject criterion).
Comparing approaches II
| estimator | fwer |
|---|---|
| t-test all | 0.22 |
| t-test all holm adj | 0.04 |
| t-test omnibus | 0.04 |
| t-test Y1 | 0.05 |
The approach using 5 tests produces a \(p < .05\) much too often — recall that there are no causal effects at all for any of these outcomes.
A test of a single outcome (here
Y1) has \(p < .05\) no more than 5% of the simulations.The omnibus test also shows a well-controlled error rate.
Using a multiple testing correction (here we use the “Holm” correction) also correctly controls the false positive rate.
The Holm correction
FYI, here is how to use the Holm correction (Notice what happens to the \(p\)-values):
p1 p2 p3 p4 p5
0.88 0.59 0.43 0.30 0.27 p1 p2 p3 p4 p5
1 1 1 1 1 ## To show what happens with "significant" p-values
theps_new <- sort(c(theps, newlowp = .01))
p.adjust(theps_new, method = "holm")newlowp p5 p4 p3 p2 p1
0.06 1.00 1.00 1.00 1.00 1.00 Multiple hypothesis testing: Multiple treatment arms
The same kind of problem can happen when the question is about the differential effects of a multi-armed treatment.
With 5 arms, “the effect of arm 1” could mean many different things: “Is the average potential outcome under arm 1 bigger than arm 2?”, “Are the potential outcomes of arm 1 bigger than the average potential outcomes of all of the other arms?”
If we just focus on pairwise comparisons across arms, we could have \(((5 \times 5) - 5)/2 = 10\) unique tests!
Multiple hypothesis testing: Multiple treatment arms
Here are some potential and observed outcomes and T with
multiple values.
ID T Y_T_2 Y_T_3 Y_T_4 Y_T_5 Y
1 001 3 0.366 0.546 -0.626 -0.125 0.546
2 002 3 0.931 -2.233 1.309 1.078 -2.233
3 003 4 -1.907 0.288 -0.133 -1.261 -0.133
4 004 5 0.052 0.544 -1.608 -0.452 -0.452
5 005 2 -0.848 -1.192 -1.308 -1.027 -0.848
6 006 3 -0.368 -0.018 -0.045 0.068 -0.018Multiple hypothesis testing: Multiple treatment arms
Here are the 10 pairwise tests with and without adjustment for multiple testing. Notice how one “significant” result (\(p=.01\)) changes with adjustment.
Comparison Stat p.value p.adjust
1 1 - 2 = 0 1.435 0.231 1.0000
2 1 - 3 = 0 0.8931 0.3447 1.0000
3 1 - 4 = 0 6.404 0.01139 0.1139
4 1 - 5 = 0 0.8216 0.3647 1.0000
5 2 - 3 = 0 0.05882 0.8084 1.0000
6 2 - 4 = 0 2.641 0.1041 0.7287
7 2 - 5 = 0 0.0437 0.8344 1.0000
8 3 - 4 = 0 3.232 0.07222 0.6500
9 3 - 5 = 0 0.0003464 0.9852 1.0000
10 4 - 5 = 0 2.899 0.08861 0.7089Approaches to testing hypotheses with multiple arms
We illustrate four different approaches:
- do all of the pairwise tests and choose the best one (a bad idea);
- do all the pairwise tests and choose the best one after adjusting the p-values for multiple testing (a fine idea but one with very low statistical power);
- test the hypothesis of no relationship between any arm (an omnibus test) and the outcome (a fine idea);
- choose one arm to focus on in advance (a fine idea).
| estimator | fwer |
|---|---|
| Choose best pairwise test | 0.238 |
| Choose best pairwise test after adjustment | 0.028 |
| Overall test | 0.034 |
| t-test T1 vs all | 0.018 |
Summary
Multiple testing problems can arise from multiple outcomes or multiple treatments (or multiple moderators/interaction terms).
Procedures for making hypothesis tests and confidence intervals can involve error. Ordinary practice controls the error rates in a single test (or single confidence interval). But multiple tests require extra work to ensure that error rates are controlled.
The loss of power arising from adjustment approaches encourages us to consider what questions we want to ask of the data. For example, if we want to know if the treatment had any effect, then a joint test or omnibus test of multiple outcomes will increase our statistical power without requiring adjustment.