Inferencia Causal
Fill In Your Name
03-09-2021
- ¿Por qué a los científicos sociales y los legisladores les deberían importar la causalidad?
- Enfoque Contrafactual de la Inferencia Causal
- Salidas Potenciales
- Salidas Potenciales
- Definición de efecto causal
- Características clave de esta definición de efecto causal
- Suponga que sabemos el valor de las dos cantidades \(Y_i(1)\) y \(Y_i(0)\) (¡esto no es posible!)
- Efecto causal promedio
- Estimaciones y preguntas causales
- Otros tipos de estimaciones que pueden interesarle
- Aleatorización de la asignación del tratamiento
- Aleatorización de la asignación del tratamiento
- Asignación aleatoria versus muestreo aleatorio
- La aleatorización es poderosa (1)
- La aleatorización es poderosa (2)
- La aleatorización es poderosa (3)
- Muestreo aleatorio
- Salidas potenciales
- Asignación aleatoria a la condición roja (1) o azul (0)
- Tres supuestos clave
- Supuesto clave: SUTVA, parte 1
- Supuesto clave: SUTVA, parte 2
- Supuesto clave: Excludibilidad
- La aleatorización es poderosa (4)
- Estudios aleatorizados frente a observacionales
¿Por qué a los científicos sociales y los legisladores les deberían importar la causalidad?
- [Discusión con ejemplos propios .]
Enfoque Contrafactual de la Inferencia Causal
Cambios recientes en la investigación en ciencias sociales
Históricamente, la causalidad inversa y el sesgo causado por variable omitidas han sido problemáticos para muchas investigaciones de las ciencias sociales que buscan hacer afirmaciones causales.
Recientemente, el enfoque contrafactual ha sido adoptado en las ciencias sociales como marco para la inferencia causal.
Esto representa un gran cambio en la investigación:
Ser más precisos sobre lo que entendemos por efectos causales.
Uso de aleatorización o de diseños que funcionan como si se hubiese aleatorizado
Más colaboraciones entre investigadores y profesionales expertos.
“X causa Y” es una afirmación sobre lo que no sucedió
En el enfoque contrafactual: “Si X no hubiera ocurrido, entonces Y no habría ocurrido”.
Los experimentos nos ayudan a aprender acerca de las afirmaciones contrafáctuales y basadas en la manipulación de la causalidad.
No está mal conceptualizar la “causa” de otra manera. Pero ha sido productivo trabajar en este marco hipotético (Brady 2008).
Cómo interpretar “X causa Y” en este enfoque
“X causa Y” no implica necesariamente que W y V no causen Y: X es parte de la historia, no toda la historia. (No se necesita conocer la historia completa para saber si X causa Y).
“X causa Y” requiere un contexto: los fósforos causan la llama pero requieren oxígeno; las aulas pequeñas mejoran los resultados de las pruebas, pero requieren profesores experimentados y financiación (Cartwright and Hardie 2012).
“X causa Y” puede significar “Si X ocurre, la probabilidad de Y es mayor que sin que X ocurra”. o “Sin que X ocurra no hay Y”. Cualquiera de las dos afirmaciones es compatible con la idea contrafactual.
Cómo interpretar “X causa Y” en este enfoque
No es necesario conocer el mecanismo para establecer que X causa Y. El mecanismo puede ser complejo y puede involucrar probabilidad: X causa Y a veces debido a A y a veces debido a B.
La causalidad contrafactual no requiere “una secuencia espacio-temporal continua de intermediarios causales”
- Ejemplo: la persona A planea el evento Y. La acción de la persona B detendría a Y (digamos, un golpe aleatorio de un extraño). La persona C no sabe sobre la persona A o la acción Y, pero detiene a B (quizá porque piensa que B se va a tropezar). Entonces, la Persona A realiza la acción Y y la Persona C causa la acción Y (sin la acción de la Persona C, Y no habría ocurrido)(Holland 1986).
Correlación no es igual a causalidad.
Ejercicio: equinácea
Su amigo dice que tomar equinácea (un remedio tradicional) reduce la duración de los resfriados.
Si adoptamos un enfoque contrafactual, ¿qué nos dice implícitamente esta afirmación sobre el contrafactual? ¿Qué otros contrafactuales podrían ser posibles y por qué?
Salidas Potenciales
Salidas Potenciales
Para cada unidad asumimos que hay dos valores posteriores al tratamiento: \(Y_i(1)\) y \(Y_i(0)\).
\(Y_i(1)\) es el resultado que obtendría la unidad si recibe el tratamiento (\(T_i = 1\)).
\(Y_i(0)\) es el resultado que obtendría la unidad si no recibe el tratamiento (\(T_i = 0\)).
Definición de efecto causal
El efecto causal del tratamiento (relativo al control) es: \(\tau_i = Y_i (1) - Y_i(0)\)
Tenga en cuenta que hemos pasado a usar \(T\) para indicar nuestro tratamiento (del cuál queremos saber el efecto). \(X\) se utilizará para las variables explicatiorias.
Características clave de esta definición de efecto causal
Debe definir la condición de control para definir un efecto causal.
- Digamos que \(T = 1\) significa una reunión comunitaria para discutir la salud pública. ¿\(T = 0\) no hay reunión en absoluto? ¿Es \(T = 0\) una reunión comunitaria sobre un tema diferente? ¿Es \(T = 0\) un volante sobre salud pública?
- La frase `` efecto causal de \(T\) en \(Y\) ’’ no tiene sentido sin saber qué significa no tener \(T\).
Cada unidad individual \(i\) tiene su propio efecto causal \(\tau_i\).
Pero no podemos medir el efecto causal a nivel individual, porque no podemos observar \(Y_i (1)\) y \(Y_i(0)\) al mismo tiempo. Esto se conoce como el problema fundamental de la inferencia causal. Lo que observamos es \(Y_i\):
\(Y_i = T_iY_i(1) + (1-T_i)Y_i(0)\)
Suponga que sabemos el valor de las dos cantidades \(Y_i(1)\) y \(Y_i(0)\) (¡esto no es posible!)
| \(i\) | \(Y_i(1)\) | \(Y_i(0)\) | \(\tau_i\) |
|---|---|---|---|
| Andrei | 1 | 1 | 0 |
| Bamidele | 1 | 0 | 1 |
| Claire | 0 | 0 | 0 |
| Deepal | 0 | 1 | -1 |
Conocemos el efecto del tratamiento para cada individuo.
Nótese la heterogeneidad en los efectos del tratamiento a nivel individual.
Pero solo sabemos del valor de una de las salidas potenciales para cada individuo como máximo, lo que significa que no conocemos estos efectos del tratamiento.
Efecto causal promedio
- Si bien no podemos medir el efecto causal individual, \(\tau_i = Y_i (1)-Y_i (0)\), podemos asignar sujetos al azar a las condiciones de tratamiento y control para estimar el efecto causal promedio, \(\bar{\tau}_i\):
\(\overline{\tau_i} = \frac{1}{N}\sum_{i = 1}^N (Y_i (1) -Y_i (0)) = \overline{Y_i (1) -Y_i (0)}\)
El efecto causal promedio también se conoce como efecto promedio del tratamiento (Average Treatment Effect, ATE).
Explicación adicional sobre cómo calcularlo después de discutir la asignación aleatoria del tratamiento en la siguiente sección.
Estimaciones y preguntas causales
Antes de discutir la aleatorización y cómo esta nos permite estimar el ATE, tenga en cuenta que el ATE es un tipo de estimando.
Un estimando es una cantidad sobre la que se desea aprender (a partir de los datos). Es el objetivo de la investigación que usted estableció.
Ser preciso con la la pregunta de investigación significa ser preciso con el estimando. Para preguntas causales, esto significa especificar:
- La variable de interés
- Las condiciones de tratamiento y control.
- La población de estudio
Otros tipos de estimaciones que pueden interesarle
El ATE para un subgrupo en particular, también conocido como efecto promedio condicional del tratamiento (CATE, conditional ATE)
Diferencias en el CATE: diferencias en el efecto promedio del tratamiento para un grupo en comparación con otro grupo.
El ATE solo para las unidades tratadas, también conocido como efecto promedio del tratamiento en los tratados (Average treatment effect on the treated, ATT)
El ATE local (Local ATE, LATE). “Local” = aquellos cuyo estado de tratamiento cambiaría por el estímulo de un diseño de estímulo (también conocido como efecto causal promedio del cumplidor o CACE, por sus siglas en inglés: complier average causal effect) o aquellos en el vecindario de una discontinuidad para un diseño de regresión discontinua.
Las estimaciones se analizan en detalle en el Módulo de estimaciones y estimadores.
Aleatorización de la asignación del tratamiento
Aleatorización de la asignación del tratamiento
La aleatorización significa que cada observación tiene una probabilidad conocida de asignación a condiciones experimentales entre 0 y 1.
- Ninguna unidad de la muestra experimental se asigna al tratamiento con total certeza (probabilidad = 1) o al control con total certeza (probabilidad = 0).
Las probabilidad de asignación al tratamiento puede variar para cada unidad.
Por ejemplo, la probabilidad puede variar según el grupo: las mujeres pueden tener un 25% de probabilidad de ser asignadas al tratamiento, mientras que los hombres tienen una probabilidad diferente.
Incluso puede variar de una persona a otra, claro está que eso complicaría el análisis.
Asignación aleatoria versus muestreo aleatorio
Aleatorización (del tratamiento): asignación de sujetos con probabilidad conocida a condiciones experimentales.
Esta asignación aleatoria de tratamiento puede combinarse con cualquier tipo de muestra (muestra aleatoria, muestra de conveniencia, etc.).
Pero el tamaño y otras características de su muestra afectarán su poder y su capacidad para extrapolar su hallazgo a otras poblaciones.
Muestreo aleatorio (de la población): selección de sujetos de una población a la muestra con probabilidad conocida.
La aleatorización es poderosa (1)
Queremos conocer el valor del ATE, \(\overline{\tau_i} = \overline{Y_i (1) -Y_i (0)}\).
Aprovecharemos el hecho de que la media de diferencias es igual a la diferencia de medias:
ATE \(= \overline{Y_i (1) -Y_i (0)} = \overline{Y_i (1)} - \overline{Y_i (0)}\)
La aleatorización es poderosa (2)
Asignamos aleatoriamente algunas de nuestras unidades al tratamiento. Para estas unidades tratadas, medimos el resultado \(Y_i | T_i = 1\), que es lo mismo que \(Y_i(1)\) para estas unidades que asignamos al tratamiento.
Debido a que estas unidades se asignaron al azar al tratamiento, estos \(Y_i = Y_i (1)\) para las unidades tratadas representan los \(Y_i(1)\) para todas nuestras unidades.
En valor esperado (o en promedio a través de experimentos repetidos (escrito \(E_R[]\))):
\(E_R [\overline {Y_i} | T_i = 1] = \overline{Y_i (1)}\).
\(\overline {Y} | T_i = 1\) es un estimador insesgado de la media poblacional de resultados potenciales bajo el tratamiento.
La misma lógica se aplica a las unidades asignadas aleatoriamente al control:
\(E_R[\overline{Y_i}| T_i = 0] = \overline{Y_i (0)}\).
La aleatorización es poderosa (3)
- Entonces podemos escribir el estimador para el ATE:
\(\hat{\overline{\tau_i}} = (\overline {Y_i(1)} | T_i = 1) - (\overline {Y_i (0)} | T_i = 0)\)
- En valor esperado, o en promedio en experimentos repetidos, \(\hat{\overline {\tau_i}}\) es igual al ATE:
\(E_R[Y_i | T_i = 1] - E_R [Y_i | T_i = 0] = \overline {Y_i (1)} - \overline{Y_i (0)}\).
- Entonces podemos tomar la diferencia de estos estimadores insesgados de \(\overline{Y_i (1)}\) y \(\overline{Y_i(0)}\) para obtener una estimación insesgada del ATE.
Muestreo aleatorio
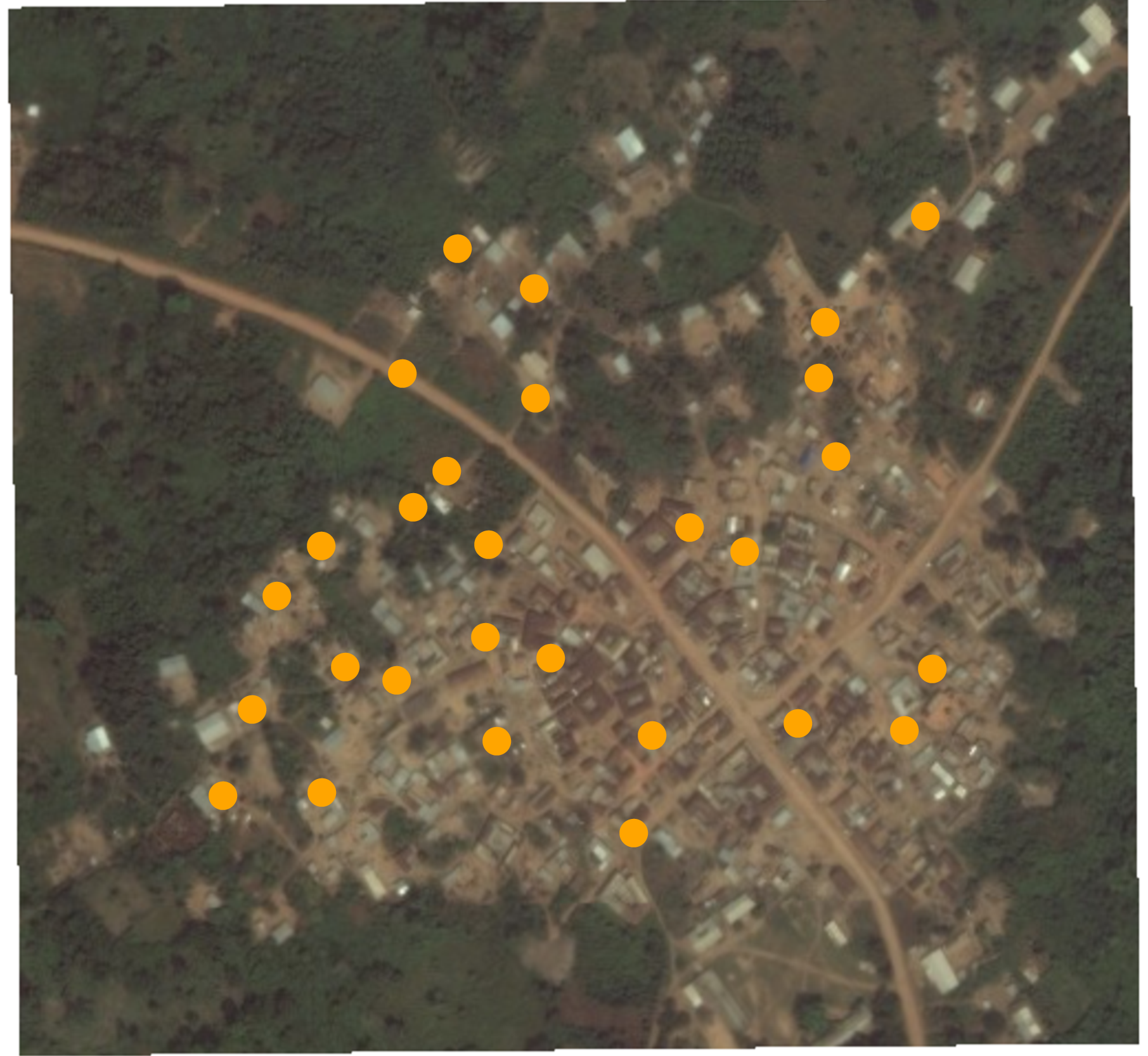
Muestreo Aleatorio de Hogares
Salidas potenciales
Cada hogar \(i\) tiene \(Y_i(1)\) and \(Y_i(0)\).
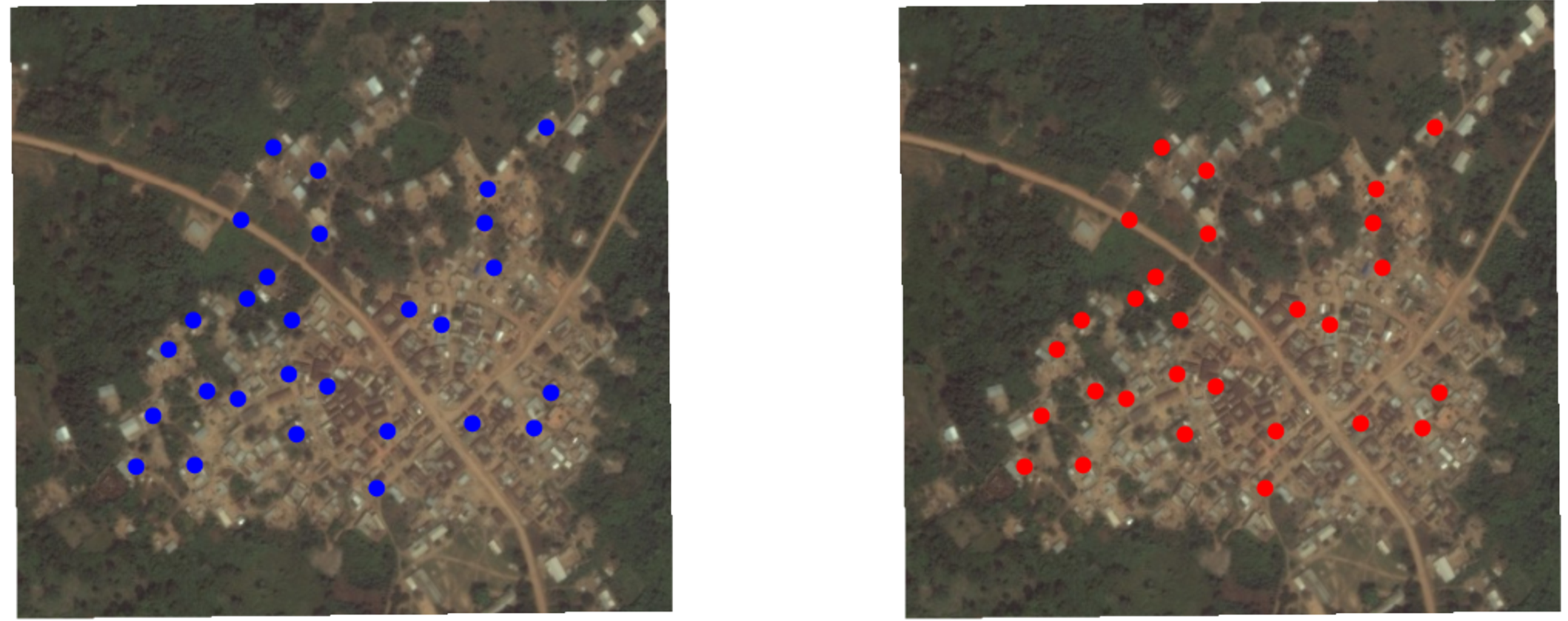
Asignación aleatoria a la condición roja (1) o azul (0)
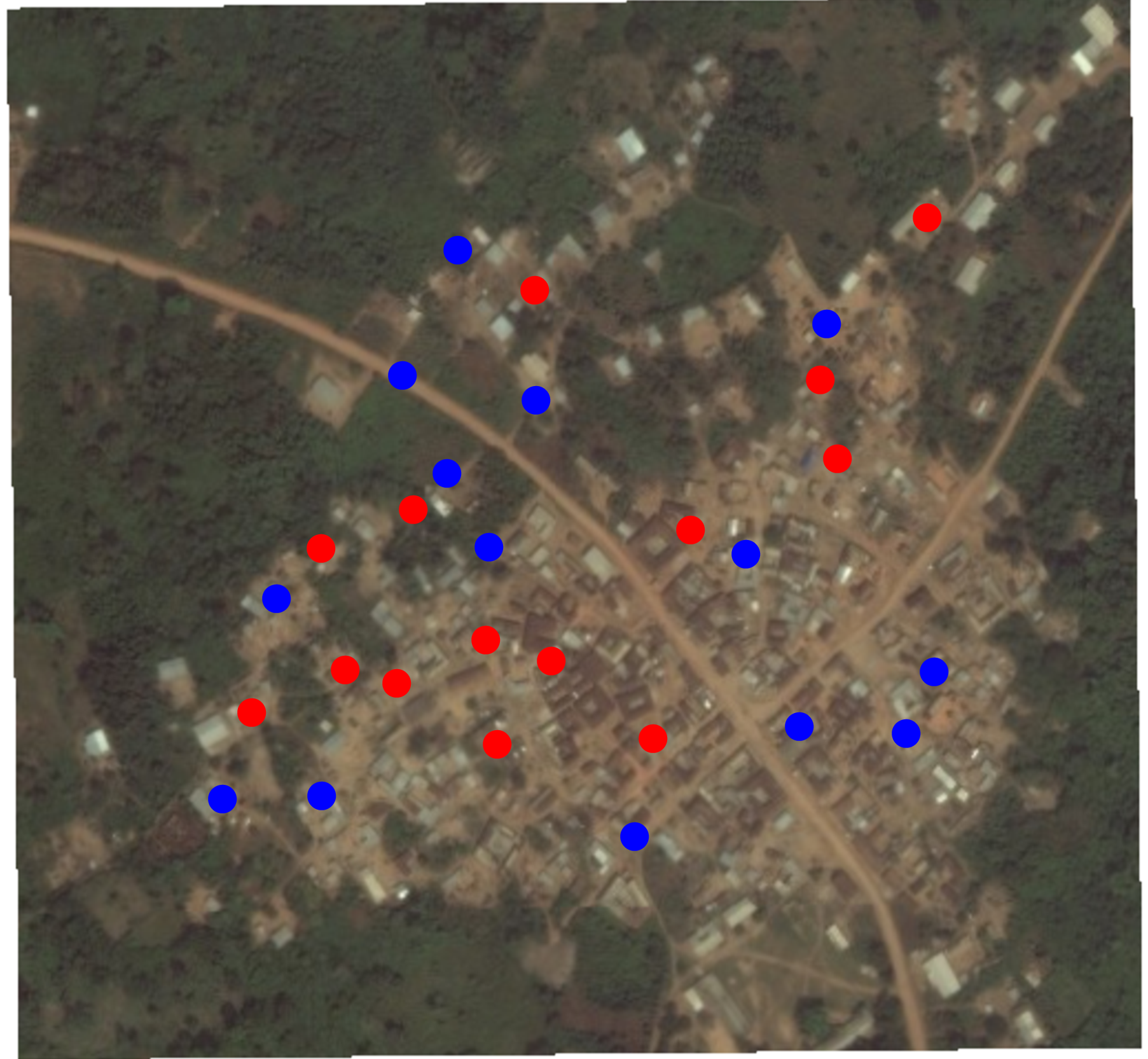
Random assignment of this random sample of households
Tres supuestos clave
Para hacer afirmaciones causales con un experimento (o para juzgar si creemos en las afirmaciones de un estudio), necesitamos tres supuestos básicos:
Asignación aleatoria de sujetos al tratamiento, lo que implica que recibir el tratamiento es estadísticamente independiente de las salidas potenciales de los sujetos.
Supuesto de estabilidad del valor bajo tratamiento para cada unidad (Stable unit treatment value assumption, SUTVA).
Excluibilidad, que significa que los valores potenciales de un sujeto responden solo al tratamiento definido y no a otros factores externos que pueden estar correlacionados con el tratamiento.
Supuesto clave: SUTVA, parte 1
No interferencia: el valor potencial de un sujeto refleja solo si ese sujeto recibe el tratamiento. No se ve afectado por cómo se asigna el tratamiento a otros sujetos.
Una violación clásica es el caso de las vacunas y sus efectos secundarios.
Imagine que yo fui asignado a la condición de control (sin vacuna). Que me enferme (\(Y_i (0)\)), depende de la asignación al tratamiento de otras personas (en caso de que sí tomen la vacuna), ¡es como si tuviera dos \(Y_i(0)\) diferentes!
SUTVA (= Supuesto de estabilidad del valor bajo el tratamiento para cada unidad )
Supuesto clave: SUTVA, parte 2
No hay variaciones ocultas del tratamiento
Digamos que el tratamiento es vacunarse, pero hay dos tipos de vacunas y tienen diferentes ingredientes.
Un ejemplo de una violación al supuesto es que el enfermarme luego de haberme puesto la vacuna (\(Y_i(1)\)) dependa de la vacuna que recibí. ¡Habría dos \(Y_i(1)\) diferentes!
Supuesto clave: Excludibilidad
La asignación al tratamiento no tiene ningún efecto sobre los resultados, excepto el que puede tener si el tratamiento se recibió.
Es importante definir el tratamiento con precisión.
Es importante también mantener la simetría entre los grupos de tratamiento y control (por ejemplo, ocultando cuál fue la asignación al tratamiento, tener los mismos procedimientos de recopilación de datos para todos los sujetos del estudio, etc.), de modo que la asignación al tratamiento solo afecte el tratamiento recibido, no otras cosas como las interacciones con los investigadores que no deberían ser parte del tratamiento.
La aleatorización es poderosa (4)
Si la intervención es aleatoria, entonces quién recibe o no la intervención no está relacionado con las características personales de los posibles destinatarios.
La aleatorización hace que aquellos que fueron seleccionados al azar para no recibir la intervención sean buenos sustitutos del contrafactual para aquellos que fueron seleccionados al azar para recibir el tratamiento, y viceversa.
Nos debemos preocupar por esto si la intervención no fue aleatorizada (= un estudio observacional).
Estudios aleatorizados frente a observacionales
Diferentes tipos de estudios
Estudios aleatorizados
- Aleatorizar el tratamiento y luego medir los resultados
Estudios observacionales
- El tratamiento no se asigna al azar. Se observa, pero no se manipula.
Ejercicio: aprendiendo acerca de sus conocimientos previos
Discutir en grupos pequeños: Ayúdeme a diseñar el próximo proyecto para responder una de estas preguntas (o una de sus propias preguntas causales). Solo plantee las características claves de dos diseños: uno observacional y el otro aleatorio.
Preguntas de investigación de ejemplo:
¿Aumentan la confianza y la coperación los proyectos de reconstrucción impulsados por la comunidad en Liberia? Ver: Nota 40 de políticas de EGAP
¿Puede el monitoreo comunitario aumentar el uso de clínicas y disminuir la mortalidad infantil en Uganda? Puede ver: Nota 58 de políticas de EGAP
Ejercicio: estudios observacionales versus estudios aleatorizados
Tareas:
Esboce un diseño de un estudio observacional ideal (sin aleatorización, sin control por parte del investigador pero con recursos infinitos para la recopilación de datos). ¿Cuáles son las preguntas que haría un lector crítico frente su afirmación de que sus resultado reflejan una relación causal?
Esboce un diseño de estudio experimental ideal (que incluya aleatorización). ¿Cuáles son las preguntas que haría un lector crítico frente su afirmación de que sus resultado reflejan una relación causal?
Discutir
¿Cuáles fueron los componentes clave y las fortalezas y debilidades de los estudios aleatorizados?
¿Cuáles fueron los componentes clave y las fortalezas y debilidades de los estudios observacionales?
Generalizabilidad y validez externa
La aleatorización aporta una alta validez interna a un estudio: confianza en que hemos aprendido el efecto causal de un tratamiento en una variable de interés.
Pero el hallazgo de un estudio en particular en un lugar particular y en un momento particular puede no ser válido en otros entornos (es decir, validez externa).
Esta es una preocupación general, no solo una preocupación para los estudios aleatorizados.
La iniciativa Metaketa de EGAP’s trabaja para acumular conocimientos mediante la planificación previa de un metanálisis de múltiples estudios que tienen una alta validez interna debido a la aleatorización.
Referencia
Nota 40 de políticas de EGAP: Asistencia para el desarollo y la capacidad de acción colectiva
Nota 50 de políticas de EGAP: ¿Funciona la rendición de cuentas que parte desde abajo?