Pruebas de hipótesis: Resumiendo información acerca de los efectos causales

Fill In Your Name

04 April 2022

El papel de las pruebas de hipótesis en la inferencia causal

Puntos clave para esta lección

  • La inferencia estadística (por ejemplo, las pruebas de hipótesis y los intervalos de confianza) requiere inferencia, es decir, razonamiento sobre lo no observado.

  • Los valores \(p\) requieren distribuciones de probabilidad.

  • Aleatorización (o diseño) + una hipótesis + una función de estadística de prueba \(\rightarrow\) distribuciones de probabilidad que representan la hipótesis (distribuciones de referencia)

  • Valores observados de las estadísticas de prueba + Distribución de referencia \(\rightarrow\) valor \(p\).

El papel de las pruebas de hipótesis en la inferencia causal

  • El problema fundamental de la inferencia causal es que sólo podemos ver una variable de resultado potencial para cualquier unidad.

  • Por lo tanto, si para Jake se produce un efecto causal contrafactual del tratamiento \(T\), cuando \(y_{text{Jake},T=1} \ne y_{text{Jake},T=0}\), entonces ¿cómo podemos aprender sobre el efecto causal?

  • Una solución es la estimación de los promedios de los efectos causales (el ATE, ITT, LATE).

  • Esto es lo que llamamos el enfoque de Neyman.

  • Otra posible solución es hacer afirmaciones o suposiciones sobre los efectos causales.

  • Podríamos decir: “Creo que el efecto sobre Jake es 5” o “Este experimento no ha tenido ningún efecto sobre nadie”. Y entonces podríamos preguntarnos “¿Cuánta evidencia tiene este experimento sobre esa afirmación?”

  • Esta evidencia se resume en un valor \(p\).

  • A esto lo llamamos enfoque de Fisher.

  • El enfoque de las pruebas de hipótesis para la inferencia causal no nos brinda una suposición, sino que nos dice cuánta evidencia o información obtenemos del diseño de la investigación sobre una afirmación causal.

  • La estimación nos permite hacer mejores suposiciones, pero no nos dice qué tanto sabemos sobre esas suposiciones.

  • Por ejemplo, una suposición con \(N=10\) parece decirnos menos sobre el efecto que \(N=1000\).

  • Por ejemplo, una suposición cuando el 95% de \(Y=1\) y el 5% de \(Y=0\) parece decirnos menos que cuando las variables de resultado se dividen por igual entre 0 y 1.

  • Casi siempre reportamos ambas, ya que esto nos ayuda a tomar decisiones: “Nuestra mejor suposición del efecto del tratamiento fue 5, y pudimos rechazar la idea de que el efecto fuera 0 (\(p\)=.01)”.

Temas básicos de las prueba de hipótesis

Componentes de una prueba de hipótesis

  • Una hipótesis es una afirmación sobre una relación entre variables de resultado potenciales.

  • Una estadística de prueba resume la relación entre el tratamiento y las variables de resultado observadas.

  • El diseño nos permite vincular la hipótesis y la estadística de prueba: podemos calcular una estadística de prueba que describa una relación entre variables de resultado potenciales.

  • El diseño también nos indica cómo generar una distribución de las posibles estadísticas de prueba sugeridas por la hipótesis.

  • Un valor \(p\) describe la relación entre nuestra estadística de prueba observada y la distribución de las posibles estadísticas de prueba hipotéticas.

Una hipótesis es una afirmación o modelo de una relación entre posibles variables de resultado

Outcome Treatment \(y_{i,0}\) ITE \(y_{i,1}\) \(Y>0\)
0 0 0 10 10 0
30 1 0 30 30 0
0 0 0 200 200 0
1 0 1 90 91 0
11 1 1 10 11 0
23 1 3 20 23 0
34 1 4 30 34 0
45 1 5 40 45 0
190 0 190 90 280 1
200 0 200 20 220 1

Por ejemplo, la hipótesis nula de ausencia de efectos, débil o tajante, es \(H_0:y_{i,1} = y_{i,0}\)

Las estadísticas de pruebas resumen las relaciones entre el tratamiento y las variables de resultado

## La estadística de prueba de diferencia de medias
meanTT <- function(ys, z) {
  mean(ys[z == 1]) - mean(ys[z == 0])
}
## Rangos de la estadística de prueba de diferencia de medias
meanrankTT <- function(ys, z) {
  ranky <- rank(ys)
  mean(ranky[z == 1]) - mean(ranky[z == 0])
}

observedMeanTT <- meanTT(ys = Y, z = T)
observedMeanRankTT <- meanrankTT(ys = Y, z = T)
observedMeanTT
[1] -49.6
observedMeanRankTT
[1] 1

El diseño conecta la estadística de prueba y la hipótesis

Lo que observamos para cada persona \(i\) (\(Y_i\)) es lo que habríamos observado en el tratamiento (\(y_{i,1}\)) o lo que habríamos observado en el control (\(y_{i,0}\)).

\[Y_i = T_i y_{i,1} + (1-T_i)* y_{i,0}\]

Entonces, si \(y_{i,1}=y_{i,0}\) por lo tanto \(Y_i = y_{i,0}\).

Lo que observamos realmente es lo que habríamos observado en la condición de control.

El diseño guía la creación de una distribución de estadísticas de prueba hipotéticas

Necesitamos saber cómo repetir nuestro experimento:

repeatExperiment <- function(N) {
  complete_ra(N)
}

Luego lo repetimos, calculando la estadística de prueba implícita por la hipótesis y el diseño cada iteración:

set.seed(123456)
possibleMeanDiffsH0 <- replicate(
  10000,
  meanTT(ys = Y, z = repeatExperiment(N = 10))
)
set.seed(123456)
possibleMeanRankDiffsH0 <- replicate(
  10000,
  meanrankTT(ys = Y, z = repeatExperiment(N = 10))
)

Planear las distribuciones de aleatoriedad bajo la hipótesis nula

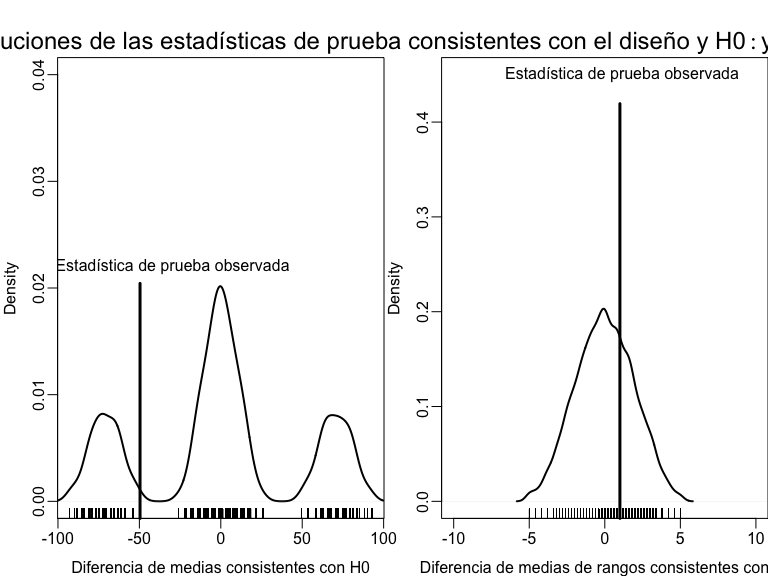
Un ejemplo de uso del diseño del experimento para probar una hipótesis con dos estadísticas de prueba diferentes.

Un ejemplo de uso del diseño del experimento para probar una hipótesis con dos estadísticas de prueba diferentes.

Los valores \(p\) resumen los planes

¿Cómo debemos interpretar los valores \(p\)? (Nótese que son de una cola)

pMeanTT <- mean(possibleMeanDiffsH0 >= observedMeanTT)
pMeanRankTT <- mean(possibleMeanRankDiffsH0 >= observedMeanRankTT)
pMeanTT
[1] 0.7785
pMeanRankTT
[1] 0.3198

Cómo hacer esto en R: COIN

## usando el paquete coin
library(coin)
set.seed(12345)
pMean2 <- coin::pvalue(oneway_test(Y ~ factor(T),
  data = dat,
  distribution = approximate(nresample = 1000), alternative = "less"
))
dat$rankY <- rank(dat$Y)
pMeanRank2 <- coin::pvalue(oneway_test(rankY ~ factor(T),
  data = dat,
  distribution = approximate(nresample = 1000), alternative = "less"
))
pMean2
[1] 0.783
99 percent confidence interval:
 0.7476 0.8157 
pMeanRank2
[1] 0.323
99 percent confidence interval:
 0.2853 0.3624

Cómo hacer esto en R: RItools

Primero instalar la versión en desarrollo del paquete de RItools

# dev_mode() ## no instalar el paquete de manera global
renv::install("markmfredrickson/RItools@randomization-distribution",
  force = TRUE
)
# dev_mode()

Luego use la función RItest.

# dev_mode()
library(RItools)
thedesignA <- simpleRandomSampler(total = N, z = dat$T, b = rep(1, N))
pMean4 <- RItest(
  y = dat$Y, z = dat$T, samples = 1000, test.stat = meanTT,
  sampler = thedesignA
)
pMeanRank4 <- RItest(
  y = dat$Y, z = dat$T, samples = 1000, test.stat = meanrankTT,
  sampler = thedesignA
)
pMean4
pMeanRank4
# dev_mode() ## and turn off dev_mode
pMean4
Call:  RItest(y = dat$Y, z = dat$T, test.stat = meanTT, sampler = thedesignA,
          samples = 1000)

                        Value Pr(>x)
Estadística de Prueba Observada -49.6   0.78

pMeanRank4
Call:  RItest(y = dat$Y, z = dat$T, test.stat = meanrankTT, sampler = thedesignA,
          samples = 1000)

                        Value Pr(>x)
Estadística de Prueba Observada     1   0.32

Cómo hacer esto en R: RI2

¿Cómo deberíamos interpretar el valor \(p\) de dos colas aquí?

## usando el paquete ri2
library(ri2)
thedesign <- declare_ra(N = N)
dat$Z <- dat$T
pMean4 <- conduct_ri(Y ~ Z,
  declaration = thedesign,
  sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMean4)
  term estimate two_tailed_p_value
1    Z    -49.6             0.4444
pMeanRank4 <- conduct_ri(rankY ~ Z,
  declaration = thedesign,
  sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMeanRank4)
  term estimate two_tailed_p_value
1    Z        1             0.6349

Siguientes temas

  • Probando hipótesis nulas débiles, \(H_0: \bar{y}_{1} = \bar{y}_{0}\).

  • Rechazando hipótesis nulas (y cometiendo errores de falsos positivos y/o falsos negativos).

  • Mantener las tasas de error de falsos positivos correctas cuando se evalúa más de una hipótesis.

  • Poder de las pruebas de hipótesis (Modulo sobre el Poder Estadístico y los Diagnósticos de Diseño).

Probando hipótesis nulas débiles

Probando las hipótesis nulas débiles de que no hay efectos promedio

  • La hipótesis nula débil es una afirmación sobre los agregados, y casi siempre se plantea en términos de promedios: \(H_0: \bar{y}_{1} = \bar{y}_{0}\)

  • La estadística de prueba para esta hipótesis es casi siempre la diferencia simple de medias (por ejemplo, el meanTT() anteriormente mencionado).

lm1 <- lm(Y ~ T, data = dat)
lm1P <- summary(lm1)$coef["T", "Pr(>|t|)"]
ttestP1 <- t.test(Y ~ T, data = dat)$p.value
library(estimatr)
ttestP2 <- difference_in_means(Y ~ T, data = dat)
c(lm1P = lm1P, ttestP1 = ttestP1, tttestP2 = ttestP2$p.value)
      lm1P    ttestP1 tttestP2.T 
    0.3321     0.3587     0.3587
  • ¿Por qué el valor \(p\) de OLS es diferente? ¿Qué supuestos utilizamos para calcularlo?

Probando las hipótesis nulas débiles de que no hay efectos promedio

Tanto la variación como la ubicación de \(Y\) cambia con el tratamiento en esta simulación.

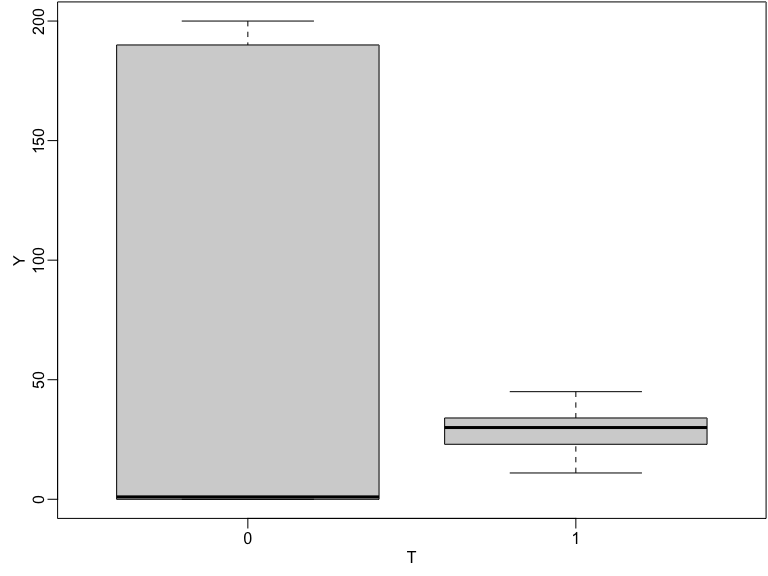
Boxplot de las variables de resultado observados por el estado de tratamiento

Boxplot de las variables de resultado observados por el estado de tratamiento

Probando las hipótesis nulas débiles de que no hay efectos promedio

## By hand:
varEstATE <- function(Y, T) {
  var(Y[T == 1]) / sum(T) + var(Y[T == 0]) / sum(1 - T)
}
seEstATE <- sqrt(varEstATE(dat$Y, dat$T))
obsTStat <- observedMeanTT / seEstATE
c(
  observedTestStat = observedMeanTT,
  stderror = seEstATE,
  tstat = obsTStat,
  pval = 2 * min(
    pt(obsTStat, df = 8, lower.tail = TRUE),
    pt(obsTStat, df = 8, lower.tail = FALSE)
  )
)
observedTestStat         stderror            tstat             pval 
        -49.6000          48.0448          -1.0324           0.3321

Rechazando hipótesis nulas

Rechazando hipótesis y creando errores

  • “Típicamente, el nivel de una prueba [\(\alpha\)] es una promesa sobre el rendimiento de esta, el tamaño es un dato sobre su rendimiento…” (Rosenbaum 2010, Glosario)

  • \(\alpha\) es la probabilidad de rechazar la hipótesis nula cuando la hipótesis nula es verdadera.

  • ¿Cómo deberíamos interpretar \(p\)=0.78? ¿Cómo deberíamos interpretar \(p\)=0.32 (nuestras pruebas de la hipótesis nula tajante)?

  • ¿Qué significa “rechazar” \(H_0: y_{i,1}=y_{i,2}\) at \(\alpha=.05\)?

Tasas de falsos positivos en las pruebas de hipótesis

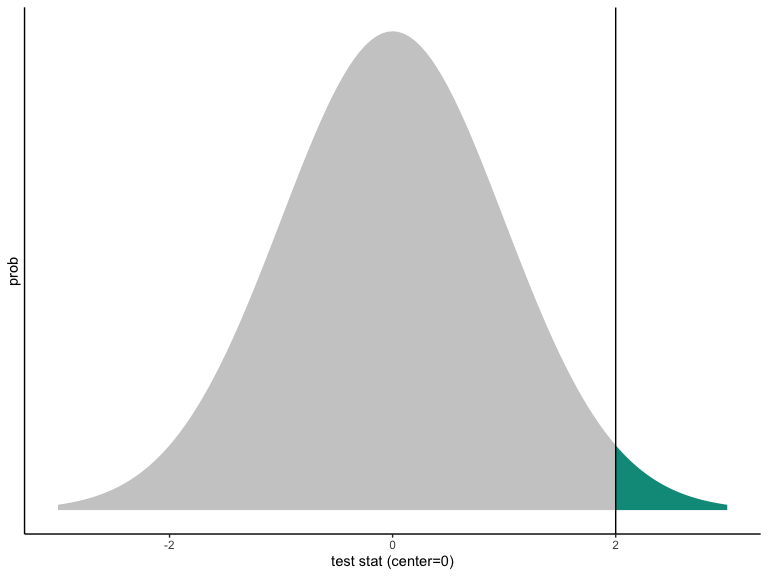
Valor p de una prueba estadística con una distribución normal.

Valor p de una prueba estadística con una distribución normal.

Nótese que:

  • La curva está centrada en el valor hipotético.

  • La curva representa el mundo de la hipótesis.

  • El valor \(p\) es lo raro que sería ver la estadística de prueba observada (o un valor más alejado del valor hipotético) en el mundo de la hipótesis nula.

  • En la imagen, el valor observado de la estadística de prueba es consistente con la distribución hipotetizada, pero no es súper consistente.

  • Incluso si \(p < .05\) (o \(p < .001\)), la estadística de prueba observada debe reflejar algún valor de la distribución hipotetizada. Esto significa que siempre se puede cometer un error al rechazar una hipótesis nula.

Errores de falsos positivos y falsos negativos

  • Si decimos: “¡El resultado experimental es significativamente diferente del valor hipotético de cero (\(p=.001\))! ¡Rechazamos la hipótesis!” cuando la verdad es cero estamos cometiendo un error de falso positivo (pretender detectar algo positivamente cuando no hay señal, sólo ruido).

  • Si decimos: “No podemos distinguir este resultado del cero (\(p=.3\)). No podemos rechazar la hipótesis de cero”. cuando la verdad no es cero estamos cometiendo un error de falso negativo (afirmando la incapacidad de detectar algo cuando hay una señal, pero está abrumada por el ruido).

Una sola prueba de una sola hipótesis

  • Una prueba de una unica hipótesis debería fomentar los errores de falsos positivos en contadas ocasiones (por ejemplo, si establecemos \(\alpha=.05\)), entonces estamos diciendo que nos sentimos cómodos con que nuestro procedimiento de prueba cometa errores de falsos positivos en no más del 5% de las pruebas de una asignación de tratamiento dada en un experimento determinado.

  • Además, una prueba única de una sola hipótesis debería detectar la señal cuando existe — debería tener un alto poder estadístico. En otras palabras, no debería fallar en la detección de una señal cuando existe (es decir, debería tener bajas tasas de error de falso negativo).

Las decisiones implican errores

  • Si los errores son inevitables, ¿cómo podemos diagnosticarlos? ¿Cómo podemos saber si nuestro proceso de comprobación de hipótesis puede generar demasiados errores de falsos positivos?

  • ¡Diagnosticar usando simulación!

Diagnosticar las tasas de falsos positivos mediante simulación

  • A través de repeticiones del diseño:

    • Cree una hipótesis nula verdadera.
    • Pruebe la hipótesis verdadera nula.
    • El valor \(p\) debe ser grande si la prueba funciona correctamente.

  • La proporción de valores \(p\) pequeños no debería ser mayor que \(\alpha\) si la prueba funciona correctamente.

Diagnosticar las tasas de falsos positivos mediante simulación

Ejemplo con un resultado binario. ¿Funciona la prueba cómo debería?

Diagnosticar falsos positivos mediante simulación

¿Cómo son los valores p cuándo no hay efecto?

collectPValues <- function(y, trt, thedistribution = exact()) {
  new_trt <- repeatExperiment(length(y)) ## Y y T no tienen relación
  thedata <- data.frame(new_trt = new_trt, y = y)
  thedata$ranky <- rank(y)
  thedata$new_trtF <- factor(thedata$new_trt)
  thelm <- lm(y ~ new_trt, data = thedata) ## Las cuatro pruebas
  t_test_CLT <- difference_in_means(y ~ new_trt, data = thedata)
  t_test_exact <- oneway_test(y ~ new_trtF,
    data = thedata,
    distribution = thedistribution
  )
  t_test_rank_exact <- oneway_test(ranky ~ new_trtF,
    data = thedata,
    distribution = thedistribution
  )
  owP <- coin::pvalue(t_test_exact)[[1]]
  owRankP <- coin::pvalue(t_test_rank_exact)[[1]]
  return(c( ## Regrese los valores p
    lmp = summary(thelm)$coef["new_trt", "Pr(>|t|)"],
    neyp = t_test_CLT$p.value[[1]],
    rtp = owP,
    rtpRank = owRankP
  ))
}

Diagnosticar las tasas de falsos positivos mediante simulación

  • Cuando no hay ningún efecto, una prueba de la hipótesis nula de ausencia de efectos debería producir un valor p grande.

  • Si la prueba funciona bien, deberíamos ver sobre todo valores p grandes y muy pocos valores p pequeños.

  • Algunos de los valores p para las cuatro pruebas diferentes (hicimos 5000 simulaciones, sólo mostramos 5)

        [,1] [,2] [,3] [,4]   [,5]
lmp        1    1    1    1 0.1411
neyp       1    1    1    1 0.1778
rtp        1    1    1    1 0.4444
rtpRank    1    1    1    1 0.4444

Diagnosticar las tasas de falsos positivos mediante simulación

De hecho, si no hay ningún efecto, y si decidimos rechazar la hipótesis nula de ausencia de efectos con \(\alpha=.25\), querríamos que no más del 25% de nuestros valores p en esta simulación sean menores que p=.25. ¿Qué podemos observar aquí? ¿Qué pruebas parecen tener tasas de falsos positivos demasiado altas?

## Calcule la proporción de valores p menores que .25, por cada fila de pDist
apply(pDist, 1, function(x) {
  mean(x < .25)
})
    lmp    neyp     rtp rtpRank 
 0.4536  0.4536  0.0000  0.0000

Diagnosticar las tasas de falsos positivos mediante simulación

Compare las pruebas trazando la proporción de valores p menores que un número determinado. Las pruebas de “inferencia aleatoria” controlan la tasa de falsos positivos (son las pruebas de uso de permutación directa, repitiendo el experimento).

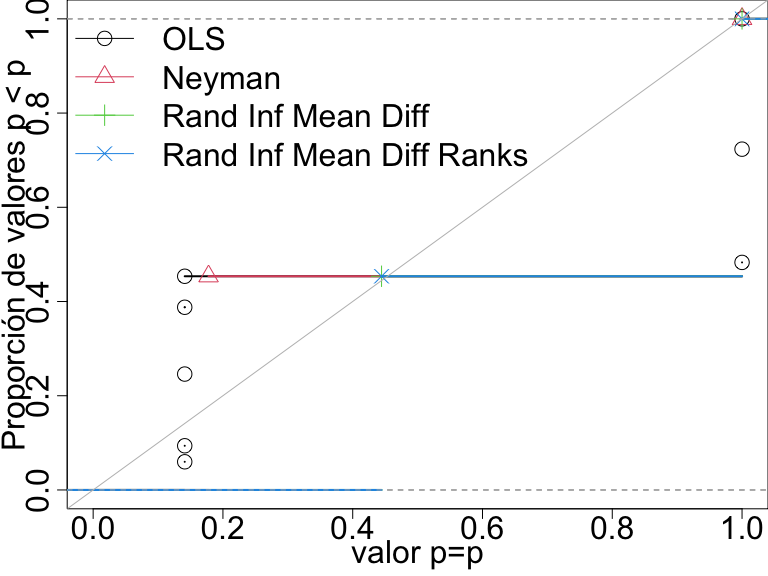
\tiny Dist. p-val para 4 pruebas cuando no hay efectos n=10. Cuando la prueba controla su tasa de falsos positivos los puntos caen sobre o por debajo de la línea diagonal.

Dist. p-val para 4 pruebas cuando no hay efectos n=10. Cuando la prueba controla su tasa de falsos positivos los puntos caen sobre o por debajo de la línea diagonal.

Tasa de falsos positivos con \(N=60\) y variable de resultado binaria

En este diseño, sólo las pruebas basadas en la inferencia de aleatorización directa controlan la tasa de falsos positivos.

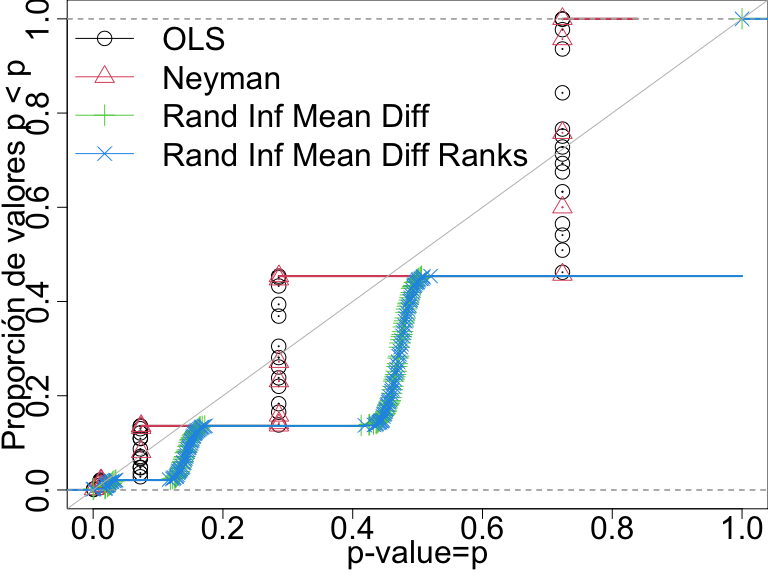
\tiny Dist. P-val para 4 pruebas cuando no hay efectos n=60 y una variable de resultado binaria. Una prueba que controla la tasa de falsos positivos debería tener puntos en la línea diagonal o por debajo de ella.

Dist. P-val para 4 pruebas cuando no hay efectos n=60 y una variable de resultado binaria. Una prueba que controla la tasa de falsos positivos debería tener puntos en la línea diagonal o por debajo de ella.

Tasa de falsos positivos con \(N=60\) y variable de resultado continua

Aquí todas las pruebas hacen un buen trabajo al controlar la tasa de falsos positivos.

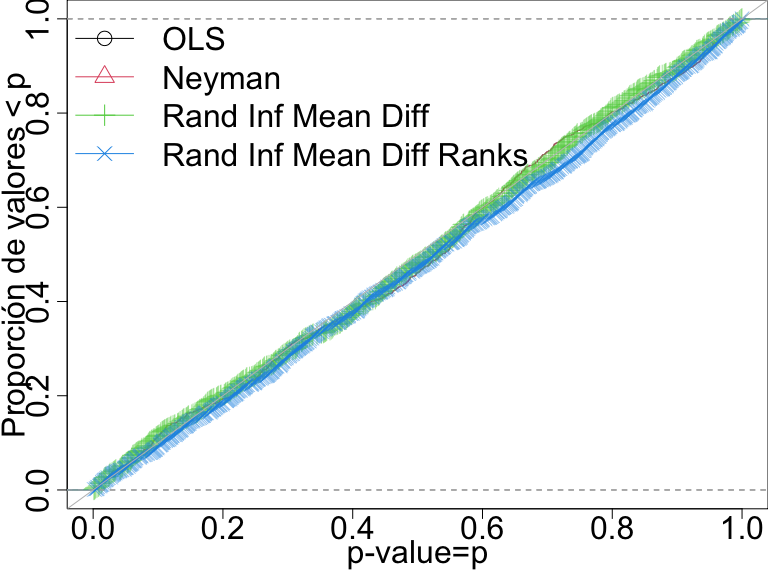
\tiny Dist. P-val para 4 pruebas cuando no hay efectos n=60 y una variable de resultado continua. Cuando la prueba que controla la tasa de falsos positivos los puntos caen sobre o debajo de la línea diagonal.

Dist. P-val para 4 pruebas cuando no hay efectos n=60 y una variable de resultado continua. Cuando la prueba que controla la tasa de falsos positivos los puntos caen sobre o debajo de la línea diagonal.

Resumen

  • Una buena prueba:

    1. raramente arroja dudas sobre la verdad, y

    2. distingue fácilmente la señal del ruido (pone en duda la falsedad con frecuencia).

  • Podemos saber si nuestro procedimiento de prueba controla las tasas de falsos positivos dado nuestro diseño.

  • Cuando las tasas de falsos positivos no están controladas, ¿qué puede estar fallando? (A menudo tiene que ver con las asintóticas).

Temas avanzados

Algunos temas avanzados relacionados con las pruebas de hipótesis

  • Incluso si un procedimiento de prueba determinado controla la tasa de falsos positivos para una sola prueba, puede que no controle la tasa para un grupo de pruebas múltiples. Léase: 10 Things you need to know about multiple comparisons para obtener una guía de los enfoques para controlar dichas tasas de rechazo en múltiples pruebas.

  • Un intervalo de confianza de \(100(1-\alpha)\) puede definirse como el rango de hipótesis en el que todos los valores \(p\) son mayores o iguales que \(alpha\). Esto se llama invertir la prueba de hipótesis (Rosenbaum (2010)). Es decir, un intervalo de confianza es una colección de pruebas de hipótesis.

Qué más debe saber sobre las pruebas de hipótesis

  • Una estimación puntual basada en pruebas de hipótesis se denomina estimación puntual de Hodges-Lehmann (Rosenbaum (1993),Hodges and Lehmann (1963)).

  • Un conjunto de pruebas de hipótesis puede combinarse en una sola prueba de hipótesis (Hansen and Bowers (2008),Caughey, Dafoe, and Seawright (2017)).

  • En las pruebas de equivalencia, se puede plantear la hipótesis de que dos estadísticas de prueba son equivalentes (es decir, el grupo de tratamiento es el mismo que el grupo de control) en lugar de una sola estadística de prueba (la diferencia entre los dos grupos es cero) (Hartman and Hidalgo (2018)).

  • Dado que una prueba de hipótesis es un modelo de variable de resultado potenciales, se puede utilizar la prueba de hipótesis para aprender sobre modelos complejos, como los modelos de propagación de los efectos del tratamiento a través de redes (Bowers, Fredrickson, and Panagopoulos (2013), Bowers, Fredrickson, and Aronow (2016), Bowers et al. (2018))

Ejercicio: Pruebas de hipótesis y estadísticas de prueba

  1. Si una intervención fue muy eficaz en el aumento de la variabilidad de una variable de resultado, pero no cambió la media, ¿sería grande o pequeño el valor \(p\) reportado por R o Stata si utilizamos lm_robust() o difference_of_means() o reg o t.test?

  2. Si una intervención hace que la media del grupo de control se reduzca moderadamente pero aumenta mucho algunas variables de resultado (como un efecto 10 veces mayor), ¿el valor \(p\) de R lm_robust() o difference_of_means() sería grande o pequeño?

Probar muchas hipótesis

¿Cuándo podríamos probar muchas hipótesis?

  • ¿Difiere el efecto de un tratamiento experimental entre los distintos grupos? ¿Podrían surgir diferencias en el efecto del tratamiento debido a algunas característicasde los sujetos experimentales?

  • ¿Qué estrategias de comunicación fueron más eficaces en una única variable de resultado?

  • ¿Cuáles, entre varias variables de resultado, fueron influenciados por una única intervención experimental?

Tasas de falsos positivos en las pruebas de hipótesis múltiples

Digamos que nuestra probabilidad de cometer un error de falso positivo es de 0,05 en una sola prueba. ¿Qué ocurre si preguntamos: (1) cuál de estos 10 resultados tiene una relación estadísticamente significativa con los dos brazos de tratamiento? o (2) cuál de estos 10 brazos de tratamiento tiene una relación estadísticamente significativa con la única variable de resultado?

  • La probabilidad de un error de falso positivo debe ser menor o igual a 0,05 en una prueba.
  • La probabilidad de un error de falso positivo debe ser menor o igual a \(1 - ( ( 1 - .05 ) \times (1 - .05) ) = .0975\) en 2 pruebas.
  • La probabilidad de al menos un error de falso positivo con \(\alpha=.05\) en 10 pruebas debería ser \(\le\) \(1 - (1-.05)^{10}=.40\).

Descubrimientos con pruebas múltiples

Número de errores hechos al probar hipótesis nulas \(m\) (Benjamini and Hochberg 1995 ’s Table 1). Las celdas son el número de pruebas. \(R\) es # de “descubrimientos” y \(V\) es # de falsos descubrimientos, \(U\) es # de no rechazos correctos, y \(S\) es # de rechazos correctos.

Declarado No significativo
Declarado
| Significativo		 Total
Hipótesis nula real (\(H_{real}=0\)) 
        U
 
      V
 \(m_0\)
Hiptsis nula falsa (\(H_{real} \ne 0\)) 
        T
 
      S
 m - \(m_0\)
Total 
       m-R
 
      R
 m

Dos tasas de error principales a controlar cuando se prueban muchas hipótesis

  1. La tasa de error familiar (FWER) es \(P(V>0)\) (Probabilidad de cualquier error de falso positivo).

    • Nos gustaría controlar esto si planeamos tomar una decisión sobre los resultados de nuestras pruebas múltiples. El proyecto de investigación es principalmente confirmatorio.

    • Véanse, por ejemplo, los proyectos de la OES http://oes.gsa.gov: las agencias federales tomarán decisiones sobre programas en función de la detección de resultados o no.

  2. La tasa de falsos descubrimientos (FDR) es \(E(V/R | R>0)\) (proporción promedio de Errores de falsos positivos dados algunos rechazos).

    • Nos gustaría controlar esto si estamos usando este experimento para planificar el próximo experimento. Estamos dispuestos a aceptar una mayor probabilidad de error en aras de darnos más posibilidades de descubrimiento.

    • Por ejemplo, se podría imaginar que una organización, un gobierno, una ONG, podría decidir llevar a cabo una serie de experimentos como parte de una “agenda de aprendizaje”: ningún experimento determina la toma de decisiones, hay más espacio para la exploración.

Nos centraremos en el FWER, pero recomendamos pensar en el FDR y en las agendas de aprendizaje como una forma muy útil de proceder.

Preguntas con variables de resultado múltiples

  • ¿Cuál es el efecto de un tratamiento sobre múltiples variables de resultado?

  • ¿En qué variables de resultado (de entre muchas) tuvo efecto el tratamiento?

  • La segunda pregunta, en particular, puede conducir al tipo de problemas de tasa de error familiar relacionadas entre sí a los que nos referimos anteriormente.

Pruebas de hipótesis múltiples: Variables de Resultado Múltiples

Imagine que tenemos cinco variables de resultado y un tratamiento (mostrando aquí las variables de resultado potenciales y observadas):

   ID T Y1_T_0 Y1_T_1 Y2_T_0 Y2_T_1 Y3_T_0 Y3_T_1 Y4_T_0 Y4_T_1 Y5_T_0 Y5_T_1
1 001 0   0.19   0.19  0.366  0.366  0.546  0.546 -0.626 -0.626 -0.125 -0.125
2 002 0  -0.43  -0.43  0.931  0.931 -2.233 -2.233  1.309  1.309  1.078  1.078
3 003 0   0.91   0.91 -1.907 -1.907  0.288  0.288 -0.133 -0.133 -1.261 -1.261
4 004 0   1.79   1.79  0.052  0.052  0.544  0.544 -1.608 -1.608 -0.452 -0.452
5 005 1   1.00   1.00 -0.848 -0.848 -1.192 -1.192 -1.308 -1.308 -1.027 -1.027
6 006 0   1.11   1.11 -0.368 -0.368 -0.018 -0.018 -0.045 -0.045  0.068  0.068
   ID T    Y1     Y2     Y3     Y4     Y5
1 001 0  0.19  0.366  0.546 -0.626 -0.125
2 002 0 -0.43  0.931 -2.233  1.309  1.078
3 003 0  0.91 -1.907  0.288 -0.133 -1.261
4 004 0  1.79  0.052  0.544 -1.608 -0.452
5 005 1  1.00 -0.848 -1.192 -1.308 -1.027
6 006 0  1.11 -0.368 -0.018 -0.045  0.068

Podemos detectar un efecto en la variable de resultado Y1?

¿Podemos detectar un efecto en la variable de resultado Y1? (es decir, ¿la prueba de hipótesis produce un valor \(p\) lo suficientemente pequeño?) 

coin::pvalue(oneway_test(Y1 ~ factor(T), data = dat1))
[1] 0.88
## Notese que el valor p de la prueba t es igual a la prueba chi al cuadrado
## valor p.
coin::pvalue(independence_test(Y1 ~ factor(T),
  data = dat1,
  teststat = "quadratic"
))
[1] 0.88

¿En cuál de las cinco variables de resultado podemos detectar un efecto?

¿En cuál de las cinco variables de resultado podemos detectar un efecto? (es decir, ¿alguna de las cinco pruebas de hipótesis produce un valor \(p\) lo suficientemente pequeño?) 

p1 <- coin::pvalue(oneway_test(Y1 ~ factor(T), data = dat1))
p2 <- coin::pvalue(oneway_test(Y2 ~ factor(T), data = dat1))
p3 <- coin::pvalue(oneway_test(Y3 ~ factor(T), data = dat1))
p4 <- coin::pvalue(oneway_test(Y4 ~ factor(T), data = dat1))
p5 <- coin::pvalue(oneway_test(Y5 ~ factor(T), data = dat1))
theps <- c(p1 = p1, p2 = p2, p3 = p3, p4 = p4, p5 = p5)
sort(theps)
  p5   p4   p3   p2   p1 
0.27 0.30 0.43 0.59 0.88

¿Podemos detectar un efecto en “cualquiera” de las cinco variables de resultado?

¿Podemos detectar un efecto en “cualquiera” de las cinco variables de resultado? (es decir, ¿ pueden las cinco pruebas de hipótesis para las cinco variables de resultado producir un valor \(p\) lo suficientemente pequeño?) 

coin::pvalue(independence_test(Y1 + Y2 + Y3 + Y4 + Y5 ~ factor(T),
  data = dat1, teststat = "quadratic"
))
[1] 0.67

¿Cuál enfoque es más probable que nos engañe con demasiados resultados “estadísticamente significativos” (5 pruebas o 1 prueba ómnibus)?

Comparación de enfoques I

Hagamos una simulación para conocer estos enfoques de prueba.

  • Vamos a (1) establecer que los verdaderos efectos causales sean 0, (2) reasignar repetidamente el tratamiento, y (3) hacer cada una de estas tres pruebas cada vez.

  • Dado que el efecto verdadero es 0, esperamos que la mayoría de los valores \(p\) sean grandes. (De hecho, nos gustaría que no más del 5% de los valores \(p\) sean mayores que \(p=.05\), si utilizamos el criterio de aceptación-rechazo \(\alpha=.05\)).

des1_sim <- simulate_design(des1_plus, sims = 1000)
res1 <- des1_sim %>%
  group_by(estimator) %>%
  summarize(fwer = mean(p.value < .05), .groups = "drop")

Comparación de enfoques II

Tasas de error familiares
estimator fwer
t-test all 0.22
t-test all holm adj 0.04
t-test omnibus 0.04
t-test Y1 0.05

  • El enfoque que utiliza 5 pruebas produce una \(p < .05\) con demasiada frecuencia — recuerde que no hay efectos causales en absoluto para ninguno de estas variables de resultado.

  • Una prueba de una sola variable de resultado (Y1) tiene \(p < .05\) en no más del 5% de las simulaciones.

  • La prueba ómnibus también muestra una tasa de error bien controlada.

  • El uso de una corrección de pruebas múltiples (aquí utilizamos la corrección de “Holm”) también controla correctamente la tasa de falsos positivos.

La corrección de Holm

Así es como se usa la corrección de Holm (Note lo que le sucede a los a los valores \(p\)):

theps
  p1   p2   p3   p4   p5 
0.88 0.59 0.43 0.30 0.27 
p.adjust(theps, method = "holm")
p1 p2 p3 p4 p5 
 1  1  1  1  1 
## Para mostrar que sucede con los valores p "significativos"
theps_new <- sort(c(theps, newlowp = .01))
p.adjust(theps_new, method = "holm")
newlowp      p5      p4      p3      p2      p1 
   0.06    1.00    1.00    1.00    1.00    1.00

Pruebas de hipótesis múltiples: Brazos de tratamiento múltiples

  • El mismo tipo de problema puede darse cuando la pregunta es sobre los efectos diferenciales de un tratamiento con múltiples brazos.

  • Con 5 brazos, “el efecto del brazo 1” podría significar muchas cosas diferentes: “¿Es la variable de resultado potencial promedio del brazo 1 más grande que la del brazo 2?”, “¿Son las variables de resultado potenciales del brazo 1 más grandes que el promedio de las variables de resultado potenciales de todos los demás brazos?”.

  • ¡Si sólo nos enfocamos en las comparaciones por pares entre brazos, podríamos tener \(((5 \times 5) - 5)/2 = 10\) pruebas únicas!

Pruebas de hipótesis múltiples: Brazos de tratamiento múltiples

Aquí hay unas potenciales variables de resultado observadas, y unos valores múltiples de T.

   ID T  Y_T_2  Y_T_3  Y_T_4  Y_T_5      Y
1 001 3  0.366  0.546 -0.626 -0.125  0.546
2 002 3  0.931 -2.233  1.309  1.078 -2.233
3 003 4 -1.907  0.288 -0.133 -1.261 -0.133
4 004 5  0.052  0.544 -1.608 -0.452 -0.452
5 005 2 -0.848 -1.192 -1.308 -1.027 -0.848
6 006 3 -0.368 -0.018 -0.045  0.068 -0.018

Pruebas de hipótesis múltiples: Brazos de tratamiento múltiples

Aquí están las 10 pruebas por pares con y sin ajuste para pruebas múltiples. Observe cómo un resultado “significativo” (\(p=.01\)) cambia con el ajuste.

   Comparison      Stat p.value p.adjust
1   1 - 2 = 0     1.435   0.231   1.0000
2   1 - 3 = 0    0.8931  0.3447   1.0000
3   1 - 4 = 0     6.404 0.01139   0.1139
4   1 - 5 = 0    0.8216  0.3647   1.0000
5   2 - 3 = 0   0.05882  0.8084   1.0000
6   2 - 4 = 0     2.641  0.1041   0.7287
7   2 - 5 = 0    0.0437  0.8344   1.0000
8   3 - 4 = 0     3.232 0.07222   0.6500
9   3 - 5 = 0 0.0003464  0.9852   1.0000
10  4 - 5 = 0     2.899 0.08861   0.7089

Enfoques para la prueba de hipótesis con múltiples brazos

Mostramos cuatro enfoques diferentes:

  1. Hacer todas las pruebas por pares y elegir la mejor (mala idea);
  2. Hacer todas las pruebas por pares y elegir la mejor después de ajustar los valores p para las pruebas múltiples (buena idea, pero con muy poco poder estadístico);
  3. probar la hipótesis de que no hay relación entre cualquier brazo (una prueba ómnibus) y la variable de resultado (buena idea);
  4. elegir un brazo en el que concentrarse de antemano (buena idea).
Enfoques para pruebas en experimentos de múltiples brazos.
estimator fwer
Escoger mejor prueba en parejas 0.238
Escoger mejor prueba en parejas después de ajuste 0.028
Prueba general 0.034
prueba t T1 vs todas 0.018

Resumen

  • Los problemas en las pruebas múltiples pueden surgir de múltiples variables de resultado o múltiples tratamientos (o múltiples moderadores/términos de interacción).

  • Los procedimientos para realizar pruebas de hipótesis e intervalos de confianza pueden implicar errores. La práctica ordinaria controla las tasas de error en una sola prueba (o en un solo intervalo de confianza). Pero las pruebas múltiples requieren trabajo adicional para garantizar que las tasas de error estén controladas.

  • La pérdida de poder derivada de los enfoques de ajuste nos obliga a considerar qué preguntas queremos hacer a los datos. Por ejemplo, si queremos saber si el tratamiento tuvo algún efecto, una prueba conjunta o una prueba ómnibus con múltiples variables de resultado aumentará nuestro poder estadístico sin necesidad de ajustes.

Referencias

Benjamini, Yoav, and Yosef Hochberg. 1995. “Controlling the false discovery rate: a practical and powerful approach to multiple testing.” Journal of the Royal Statistical Society 57 (1): 289–300. http://www.jstor.org/stable/2346101.
Bowers, Jake, Bruce A Desmarais, Mark Frederickson, Nahomi Ichino, Hsuan-Wei Lee, and Simi Wang. 2018. “Models, Methods and Network Topology: Experimental Design for the Study of Interference.” Social Networks 54: 196–208.
Bowers, Jake, Mark M Fredrickson, and Costas Panagopoulos. 2013. “Reasoning about Interference Between Units: A General Framework.” Political Analysis 21 (1): 97–124.
Bowers, Jake, Mark Fredrickson, and Peter M Aronow. 2016. “Research Note: A More Powerful Test Statistic for Reasoning about Interference Between Units.” Political Analysis 24 (3): 395–403.
Caughey, Devin, Allan Dafoe, and Jason Seawright. 2017. “Nonparametric Combination (NPC): A Framework for Testing Elaborate Theories.” The Journal of Politics 79 (2): 688–701.
Hansen, Ben B., and Jake Bowers. 2008. “Covariate Balance in Simple, Stratified and Clustered Comparative Studies.” Statistical Science 23 (2): 219–36.
Hartman, Erin, and F Daniel Hidalgo. 2018. “An Equivalence Approach to Balance and Placebo Tests.” American Journal of Political Science 62 (4): 1000–1013.
Hodges, J. L., and E. L. Lehmann. 1963. “Estimates of location based on rank tests.” Ann. Math. Statist 34: 598–611.
Rosenbaum, Paul R. 1993. “Hodges-Lehmann Point Estimates of Treatment Effect in Observational Studies.” Journal of the American Statistical Association 88 (424): 1250–53.
———. 2010. “Design of observational studies.” Springer Series in Statistics.