Poder estadístico
Fill In Your Name
02-03-2022
¿Qué es el poder estadístico?
¿Qué es el poder estadístico?
Queremos separar la señal del ruido.
Poder = probabilidad de rechazar la hipótesis nula, dado un efecto real \(\ne\) 0.
En otras palabras, es la habilidad de detectar un efecto en caso que el efecto exista.
Formalmente: (1 - Type II) tasa de error.
Por lo tanto, el poder está \(\in\) (0, 1).
Márgenes estándar: 0.8 or 0.9.
Puntos de partida para el análisis de poder
El análisis de poder es algo que hacemos antes de realizar un estudio
Nos ayuda a definir el tamaño de la muestra que se requiere para detectar un efecto de un tamaño dado.
O también nos ayuda a encontrar cuál es el efecto detectable mínimo para un tamaño de muestra fijo.
Esta información nos puede ayudar a decidir si vale la pena hacer el estudio o no.
No se puede aprender mucho de un estudio con hallazgos nulos y poco poder.
- ¿Hay en realidad un efecto, pero no pudimos detectarlo? ¿O en realidad no hay efecto? No podemos diferenciar.
Poder
Supongamos que el tratamiento sí produce un efecto y que realizamos el experimento muchas veces. ¿Qué tan frecuentemente obtendríamos resultados estadísticamente significativos?
Algunas cantidades estimadas que nos pueden pueden ayudar a resolver esta pregunta:
¿Qué tan grande es el efecto?
¿Cuántas unidades fueron tratadas? ¿Para cuántas se tomaron datos?
¿Qué tanto ruido hay en las mediciones de su variable de resultado?
Métodos para calcular el poder estádistico
Cálculos analíticos de poder
Simulaciones
Herramientas para el calculo del poder
Interactivas
Paquetes de R
DeclareDesign, see also https://declaredesign.org/
Cálculos analíticos de poder
Cálculos analíticos de poder
Fórmula: \[\begin{align*} \text{Poder} &= \Phi\left(\frac{|\tau| \sqrt{N}}{2\sigma}- \Phi^{-1}(1- \frac{\alpha}{2})\right) \end{align*}\]
Componentes:
- \(\phi\): la función acumulada de probabilidad (CDF) de la normal estándar crece monotónicamente
- \(\tau\): el tamaño del efecto
- \(N\): el tamaño de la muestra
- \(\sigma\): la desviación estándar de la variable dependiente
- \(\alpha\): el nivel de significancia (normalmente 0.05)
Ejemplo: Cálculos analíticos de poder
# Poder para un estudio con 80 obs y
# un tamaño del efecto de 0.25
library(pwr)
pwr.t.test(
n = 40, d = 0.25, sig.level = 0.05,
power = NULL, type = c(
"two.sample",
"one.sample", "paired"
)
)
Two-sample t test power calculation
n = 40
d = 0.25
sig.level = 0.05
power = 0.1972
alternative = two.sided
NOTE: n is number in *each* groupLimitaciones del cálculo analítico del poder
Sólo se puede derivar para algunos estadísticos de prueba (diferencia de medias)
Implica supuestos específicos acerca del proceso de generación de datos
Incompatible con diseños más complejos
Cálculo del poder basado en simulación
Cálculo del poder basado en la simulación
Debemos crear datos artificiales y simular el diseño de la investigación
También es necesario hacer supuestos para simular, pero estos los definen ustedes mismos.
Para ver cómo se hace esto en DeclareDesign, vea https://declaredesign.org/
Pasos
Definir la muestra y las funciones de los resultados potenciales.
Definir el procedimiento de asignación a tratamientos.
Crear datos artificiales
Asignar el tratamiento y luego estimar el efecto
Repetir estos pasos muchas veces
Ejemplos
Aleatorizaciçon completa
Con covariables
Con aleatorización por conglomerados
Ejemplo: Poder basado en simulaciones con aleatorización completa
# install.packages("randomizr")
library(randomizr)
library(estimatr)
## Y0 es fijo en la mayoría de experimentos .
## Entonces sólo hace falta generarlo una vez:
make_Y0 <- function(N) {
rnorm(n = N)
}
repeat_experiment_and_test <- function(N, Y0, tau) {
Y1 <- Y0 + tau
Z <- complete_ra(N = N)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z)
pval <- estimator$p.value[2]
return(pval)
}Ejemplo: Poder basado en simulaciones con aleatorización completa
power_sim <- function(N, tau, sims) {
Y0 <- make_Y0(N)
pvals <- replicate(
n = sims,
repeat_experiment_and_test(N = N, Y0 = Y0, tau = tau)
)
pow <- sum(pvals < .05) / sims
return(pow)
}
set.seed(12345)
power_sim(N = 80, tau = .25, sims = 100)[1] 0.15[1] 0.21Ejemplo: Usando DeclareDesign
library(DeclareDesign)
library(tidyverse)
P0 <- declare_population(N, u0 = rnorm(N))
# declarar Y(Z=1) y Y(Z=0)
O0 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
# assigar m unidades al tratamiento
# A0 <- declare_assignment(m=round(N/2))
A0 <- declare_assignment(Z = conduct_ra(N = N, m = round(N / 2)))
# inquiry es la diferencia promedio entreY(Z=1) y Y(Z=0)
estimand_ate <- declare_inquiry(ATE = mean(Y_Z_1 - Y_Z_0))
R0 <- declare_reveal(Y, Z)
design0_base <- P0 + A0 + O0 + R0
## Por ejemplo:
design0_N100_tau25 <- redesign(design0_base, N = 100, tau = .25)
dat0_N100_tau25 <- draw_data(design0_N100_tau25)
head(dat0_N100_tau25) ID u0 Z Y_Z_0 Y_Z_1 Y
1 001 -0.2060 0 4.794 5.044 4.794
2 002 -0.5875 0 4.413 4.663 4.413
3 003 -0.2908 1 4.709 4.959 4.959
4 004 -2.5649 0 2.435 2.685 2.435
5 005 -1.8967 0 3.103 3.353 3.103
6 006 -1.6401 1 3.360 3.610 3.610[1] 0.25[1] 0.5569(Intercept) Z
4.8458 0.5569 E0 <- declare_estimator(Y ~ Z,
model = lm_robust, label = "t test 1",
inquiry = "ATE"
)
t_test <- function(data) {
test <- with(data, t.test(x = Y[Z == 1], y = Y[Z == 0]))
data.frame(statistic = test$statistic, p.value = test$p.value)
}
T0 <- declare_test(handler = label_test(t_test), label = "t test 2")
design0_plus_tests <- design0_base + E0 + T0
design0_N100_tau25_plus <- redesign(design0_plus_tests, N = 100, tau = .25)
## Sólo repetimos la asignación aleatoria, no generamos de nuevo Y0. Ignoren la advertencia
names(design0_N100_tau25_plus)[1] "P0" "A0" "O0" "R0" "t test 1" "t test 2"design0_N100_tau25_sims <- simulate_design(design0_N100_tau25_plus,
sims = c(1, 100, 1, 1, 1, 1)
) # only repeat the random assignmentWarning: We recommend you choose a higher number of simulations than 1 for the top level of simulation.# design0_N100_tau25_sims tiene 200 filas (2 pruebas * 100 asignaciones aleatorias)
# veámos las primeras 6 filas
head(design0_N100_tau25_sims) design N tau sim_ID estimator term estimate std.error statistic p.value conf.low conf.high df outcome inquiry
1 design0_N100_tau25_plus 100 0.25 1 t test 1 Z 0.1108 0.2150 0.5153 0.60752 -0.3158 0.5374 98 Y ATE
2 design0_N100_tau25_plus 100 0.25 1 t test 2 <NA> NA NA 0.5153 0.60754 NA NA NA <NA> <NA>
3 design0_N100_tau25_plus 100 0.25 2 t test 1 Z 0.2458 0.2154 1.1411 0.25661 -0.1817 0.6733 98 Y ATE
4 design0_N100_tau25_plus 100 0.25 2 t test 2 <NA> NA NA 1.1411 0.25662 NA NA NA <NA> <NA>
5 design0_N100_tau25_plus 100 0.25 3 t test 1 Z 0.5463 0.2133 2.5608 0.01197 0.1229 0.9697 98 Y ATE
6 design0_N100_tau25_plus 100 0.25 3 t test 2 <NA> NA NA 2.5608 0.01203 NA NA NA <NA> <NA>
step_1_draw step_2_draw
1 1 1
2 1 1
3 1 2
4 1 2
5 1 3
6 1 3# para cada estimador, poder = proporción de las simulaciones con p.value < 0.5
design0_N100_tau25_sims %>%
group_by(estimator) %>%
summarize(pow = mean(p.value < .05), .groups = "drop")# A tibble: 2 × 2
estimator pow
<chr> <dbl>
1 t test 1 0.2
2 t test 2 0.2Poder con ajuste de covariables
Ajuste de covariables y poder
El ajuste de covariables puede mejorar el poder porque absorbe la variación de la variable de resultado.
Sí es para pronóstico, el ajuste de covariables puede reducir la varianza significativamente. Una menor varianza se traduce en más poder.
Sí no es para pronóstico, las ganancias en poder son mínimas.
Todas las variables tienen que ser pre-tratamiento. No eliminen observaciones a cuenta de datos faltantes.
- Ver el módulo de amenazas a la validez interna y las 10 cosas que debe saber sobre el ajuste de covariables.
El sesgo de Freedman a medida que el n muestral disminuye y el número de covariables aumenta.
Bloques
Bloques: asignar el tratamiento al azar dentro de los bloques
Ajuste de covariables “ex-ante”
Más precisión/eficiencia significa más poder
Reducir “el sesgo condicional”: relación entre el tratamiento y los resultados potenciales
Beneficios de usar bloques en vez de ajuste de covariables más evidente para experimentos pequeños.
Ejemplo: Poder basado en simulaciones con una covariable
## Y0 es fijo en la mayoría de experimentos. Solo lo generamos una vez
make_Y0_cov <- function(N) {
u0 <- rnorm(n = N)
x <- rpois(n = N, lambda = 2)
Y0 <- .5 * sd(u0) * x + u0
return(data.frame(Y0 = Y0, x = x))
}
## X predice Y0 moderadamente
test_dat <- make_Y0_cov(100)
test_lm <- lm_robust(Y0 ~ x, data = test_dat)
summary(test_lm)
Call:
lm_robust(formula = Y0 ~ x, data = test_dat)
Standard error type: HC2
Coefficients:
Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
(Intercept) 0.11 0.1880 0.585 0.559753653 -0.263 0.483 98
x 0.44 0.0814 5.413 0.000000441 0.279 0.602 98
Multiple R-squared: 0.231 , Adjusted R-squared: 0.223
F-statistic: 29.3 on 1 and 98 DF, p-value: 0.000000441## ahora la simulación
repeat_experiment_and_test_cov <- function(N, tau, Y0, x) {
Y1 <- Y0 + tau
Z <- complete_ra(N = N)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z + x, data = data.frame(Y0, Z, x))
pval <- estimator$p.value[2]
return(pval)
}
## crear los datos una vez, asigna aleatoriamente el tratamiento sims veces
## reporta qué proporción tiene p <0.05
power_sim_cov <- function(N, tau, sims) {
dat <- make_Y0_cov(N)
pvals <- replicate(n = sims, repeat_experiment_and_test_cov(
N = N,
tau = tau, Y0 = dat$Y0, x = dat$x
))
pow <- sum(pvals < .05) / sims
return(pow)
}[1] 0.13[1] 0.19Poder para la aleatorización por conglomerados
Poder y diseños de conglomerados
Recordemos el módulo de aleatorización.
Dado un \(N\) fijo, un diseño de conglomerados tiene menos poder que un diseño sin conglomerados
- La diferencia suele ser sustancial.
Tenemos que estimar la varianza correctamente:
- Errores estándar para conglomerados (lo habitual)
- Inferencia basada en la aleatorización (Randomization inference)
Para aumentar el poder:
- Es mejor aumentar el número de conglomerados que el número de unidades por conglomerados.
- Cuánto reducen el poder los conglomerados depende fundamentalmente de la correlación intra-clase (la relación entre la varianza dentro de los conglomerados y la varianza total).
Una nota sobre los conglomerados en la investigación observacional
A menudo se pasa por alto lo que conduce (posiblemente) a una incertidumbre altamente subestimada.
Inferencia frecuentista basada en la proporción \(\hat{\beta}/ \hat{se}\)
Si subestimamos \(\hat{se}\), es mucho más probable que rechacemos \(H_0\). (La tasa de error de tipo I es demasiado alta).
Muchos diseños de observación tienen mucha menos poder de lo que pensamos.
Ejemplo: Poder basado en la simulación para la aleatorización por conglomerados
## Y0 es fijo en la mayoría de experimentos. Solo lo generamos una vez
make_Y0_clus <- function(n_indivs, n_clus) {
# n_indivs número de personas por conglomerados
# n_clus número de conglomerados
clus_id <- gl(n_clus, n_indivs)
N <- n_clus * n_indivs
u0 <- fabricatr::draw_normal_icc(N = N, clusters = clus_id, ICC = .1)
Y0 <- u0
return(data.frame(Y0 = Y0, clus_id = clus_id))
}
test_dat <- make_Y0_clus(n_indivs = 10, n_clus = 100)Ejemplo: Poder basado en la simulación para la aleatorización por conglomerados
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 100
10 Ejemplo: Poder basado en la simulación para la aleatorización por conglomerados
[1] 0.09655repeat_experiment_and_test_clus <- function(N, tau, Y0, clus_id) {
Y1 <- Y0 + tau
# aqui aleatorizamos al nivel del conglomerados
Z <- cluster_ra(clusters = clus_id)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z,
clusters = clus_id,
data = data.frame(Y0, Z, clus_id), se_type = "CR2"
)
pval <- estimator$p.value[2]
return(pval)
}
power_sim_clus <- function(n_indivs, n_clus, tau, sims) {
dat <- make_Y0_clus(n_indivs, n_clus)
N <- n_indivs * n_clus
pvals <- replicate(
n = sims,
repeat_experiment_and_test_clus(
N = N, tau = tau,
Y0 = dat$Y0, clus_id = dat$clus_id
)
)
pow <- sum(pvals < .05) / sims
return(pow)
}[1] 0.66[1] 0.68Ejemplo: Poder basado en la simulación para la aleatorización por conglomerados (DeclareDesign)
P1 <- declare_population(
N = n_clus * n_indivs,
clusters = gl(n_clus, n_indivs),
u0 = draw_normal_icc(N = N, clusters = clusters, ICC = .2)
)
O1 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
A1 <- declare_assignment(Z = conduct_ra(N = N, clusters = clusters))
estimand_ate <- declare_inquiry(ATE = mean(Y_Z_1 - Y_Z_0))
R1 <- declare_reveal(Y, Z)
design1_base <- P1 + A1 + O1 + R1 + estimand_ate
## Por ejemplo:
design1_test <- redesign(design1_base,
n_clus = 10,
n_indivs = 100, tau = .25
)
test_d1 <- draw_data(design1_test)
# confirma que todos los individuos en los conglomerados fueron
# asignados al mismo tratamiento
with(test_d1, table(Z, clusters)) clusters
Z 1 2 3 4 5 6 7 8 9 10
0 100 0 100 100 100 0 0 100 0 0
1 0 100 0 0 0 100 100 0 100 100# tres estimadores, se diferencias en se_type:
E1a <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "CR2", label = "CR2 cluster t test",
inquiry = "ATE"
)
E1b <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "CR0", label = "CR0 cluster t test",
inquiry = "ATE"
)
E1c <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "stata", label = "stata RCSE t test",
inquiry = "ATE"
)
design1_plus <- design1_base + E1a + E1b + E1c
design1_plus_tosim <- redesign(design1_plus,
n_clus = 10,
n_indivs = 100, tau = .25
)## Solo repite la asignación aleatoria, no la creación de Y0.
## Ignorar la advertencia
## Querríamos más simulaciones en la práctica.
set.seed(12355)
design1_sims <- simulate_design(design1_plus_tosim,
sims = c(1, 1000, rep(1, length(design1_plus_tosim) - 2))
)Warning: We recommend you choose a higher number of simulations than 1 for the top level of simulation.design1_sims %>%
group_by(estimator) %>%
summarize(
pow = mean(p.value < .05),
coverage = mean(estimand <= conf.high & estimand >= conf.low),
.groups = "drop"
)# A tibble: 3 × 3
estimator pow coverage
<chr> <dbl> <dbl>
1 CR0 cluster t test 0.155 0.911
2 CR2 cluster t test 0.105 0.936
3 stata RCSE t test 0.131 0.918library(DesignLibrary)
## Puede que esto sea más simple que lo anterior
d1 <- block_cluster_two_arm_designer(
N_blocks = 1,
N_clusters_in_block = 10,
N_i_in_cluster = 100,
sd_block = 0,
sd_cluster = .3,
ate = .25
)
d1_plus <- d1 + E1b + E1c
d1_sims <- simulate_design(d1_plus, sims = c(1, 1, 1000, 1, 1, 1, 1, 1))Warning: We recommend you choose a higher number of simulations than 1 for the top level of simulation.d1_sims %>%
group_by(estimator) %>%
summarize(
pow = mean(p.value < .05),
coverage = mean(estimand <= conf.high & estimand >= conf.low),
.groups = "drop"
)# A tibble: 3 × 3
estimator pow coverage
<chr> <dbl> <dbl>
1 CR0 cluster t test 0.209 0.914
2 estimator 0.143 0.941
3 stata RCSE t test 0.194 0.925Estática comparada
Estática comparada
- El poder:
- Crece en función \(N\)
- Crece en función \(|\tau|\)
- Decrece en función \(\sigma\)
Poder segun el tamaño de la muestra
some_ns <- seq(10, 800, by = 10)
pow_by_n <- sapply(some_ns, function(then) {
pwr.t.test(n = then, d = 0.25, sig.level = 0.05)$power
})
plot(some_ns, pow_by_n,
xlab = "Sample Size",
ylab = "Power"
)
abline(h = .8)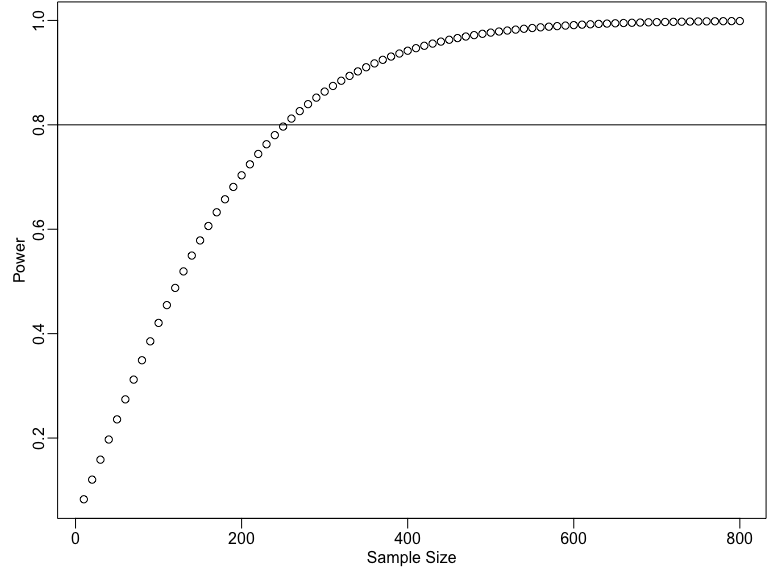
Poder segun el tamaño de la muestra
some_taus <- seq(0, 1, by = .05)
pow_by_tau <- sapply(some_taus, function(thetau) {
pwr.t.test(n = 200, d = thetau, sig.level = 0.05)$power
})
plot(some_taus, pow_by_tau,
xlab = "Efecto promedio del tratamiento (Estandarizada)",
ylab = "Poder"
)
abline(h = .8)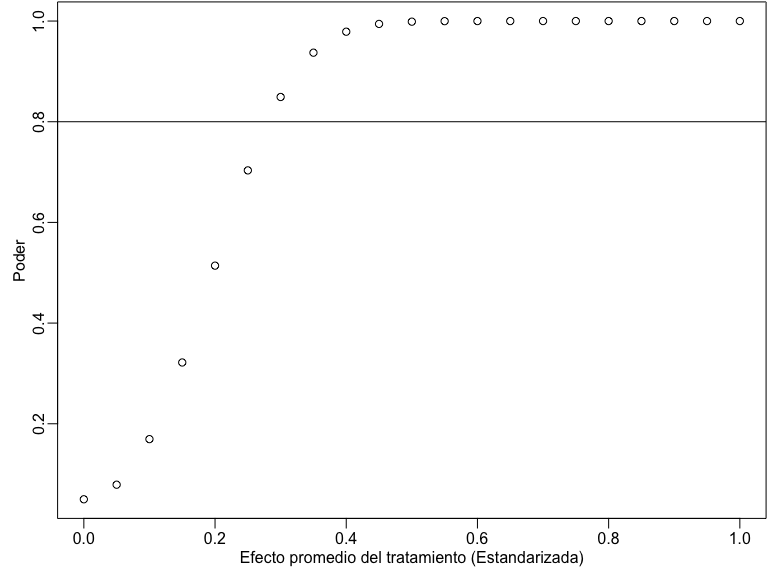
Calculadora de Poder de EGAP
Pueden usar la calculadora aquí: https://egap.shinyapps.io/power-app/
Para diseños por conglomerados puede probar ajustando:
- El número de conglomerados
- El número de unidades por conglomerados
- Correlación Intra-clase
- Efecto del tratamiento
Conclusión: Cómo mejorar el poder
Aumenten el tamaño de la muestra, \(N\)
- Si hay conglomerados, aumenten el número de conglomerados de ser posible
Intensifiquen el tratamiento
Mejoren la precisión
Ajuste de covariables
Bloques
Midan la variable de resultado correctamente
Comments
Deben conocer bien la variable de resultado
¿Cuáles son los efectos que esperan del tratamiento?
¿Cuál es el rango de variación posible que puede tener la variable de resultado?