Inférence causale
Mettre votre nom
02-03-2022
- Pourquoi les chercheurs en sciences sociales et les décideurs politiques doivent-ils se soucier de la causalité ?
- Approche contrefactuelle de l’inférence causale
- Résultats potentiels
- Randomisation de
l’assignation du traitement
- Randomisation de l’assignation du traitement
- Assignation aléatoire vs. échantillonnage aléatoire
- La randomisation est puissante (1)
- La randomisation est puissante (2)
- La randomisation est puissante (3)
- Échantillonnage aléatoire
- Résultats potentiels
- Assignation aléatoire à la condition rouge (1) ou bleue (0)
- Trois hypothèses clés
- Hypothèses clé : SUTVA, partie 1
- Hypothèses clé : SUTVA, partie 2
- Hypothèses clé : l’exclusion
- La randomisation est puissante (4)
- Études aléatoires vs. observationnelles
Pourquoi les chercheurs en sciences sociales et les décideurs politiques doivent-ils se soucier de la causalité ?
- [Discussion avec vos propres exemples.]
Approche contrefactuelle de l’inférence causale
Évolutions récentes dans la recherche en sciences sociales
Historiquement, la causalité inverse et le biais de variable omise ont posé problème pour la recherche en sciences sociales qui prétend expliquer les causes.
Récemment, l’approche contrefactuelle a été adoptée dans les sciences sociales comme cadre d’inférence causale.
Cela représente un grand changement dans la recherche :
Être plus précis sur ce que nous entendons par effet causal.
Utilisation de la randomisation ou de conceptions approchantes.
Plus de partenariats entre chercheurs.
“X cause Y” est une affirmation sur ce qui n’a pas eu lieu
Dans l’approche contrefactuelle : “Si X n’avait pas eu lieu, alors Y n’aurait pas eu lieu.”
Les expériences nous aident à en apprendre davantage sur les assertions causales, quelles soient contrefactuelles ou dues à une manipulation.
Ce n’est pas incorrect de conceptualiser la “cause” d’une autre manière. Mais il est productif de travailler dans ce cadre contrefactuel (Brady 2008).
Comment interpréter “X cause Y” dans cette approche
Ce n’est pas nécessaire de connaître le mécanisme pour établir que X cause Y. Le mécanisme peut être complexe, et il peut impliquer des probabilités : X cause Y parfois à cause de A et parfois à cause de B.
La causalité contrefactuelle ne nécessite pas “une séquence spatiotemporelle continue d’intermédiaires causaux”
- Ex : la personne A planifie l’événement Y. L’action de la personne B arrêterait Y (i.e. B va bousculer A dans la rue). La personne C ne connaît pas la personne A ou l’action Y mais arrête B (elle pense peut-être que B va trébucher). Ainsi, la personne A effectue l’action Y. Et la personne C provoque l’action Y (sans l’action de la personne C, Y n’aurait pas eu lieu)
Corrélation n’est pas causalité.
Exercice : Échinacée
Votre ami dit que la prise d’échinacée (un remède traditionnel) réduit la durée des rhumes.
Si nous adoptons une approche contrefactuelle, qu’implique cet énoncé implicitement à propos du contrefactuel ? Quels autres contrefactuels pourraient être possibles et pourquoi ?
Résultats potentiels
Résultats potentiels
Pour chaque unité, nous supposons qu’il y a deux résultats post-traitement : \(Y_i(1)\) et \(Y_i(0)\).
\(Y_i(1)\) est le résultat qu’on obtiendrait si l’unité recevait le traitement (\(T_i=1\)).
\(Y_i(0)\) est le résultat qu’on obtiendrait si l’unité recevait le contrôle (\(T_i=0\)).
Définition de l’effet causal
L’effet causal du traitement (par rapport au contrôle) est : \(\tau_i = Y_i(1) - Y_i(0)\)
Notez que nous utilisons maintenant \(T\) pour indiquer notre traitement (ce dont nous voulons étudier l’effet). \(X\) sera utilisé pour les variables de base.
Principales caractéristiques de cette définition de l’effet causal
Vous devez définir la condition de contrôle pour définir un effet causal.
- Disons que \(T=1\) signifie une réunion communautaire pour discuter de santé publique. Est-ce que \(T=0\) signifie pas de réunion ? Est-ce que \(T=0\) signifie une réunion sur un autre sujet ? Est-ce que \(T=0\) est un dépliant sur la santé publique ?
- L’expression ``effet causal de \(T\) sur \(Y\)’’ n’a pas de sens sans savoir ce que signifie ne pas avoir \(T\).
Chaque unité \(i\) a son propre effet causal \(\tau_i\).
Mais nous ne pouvons pas mesurer l’effet causal au niveau individuel, car nous ne pouvons pas observer à la fois \(Y_i(1)\) et \(Y_i(0)\) en même temps. C’est ce qu’on appelle le problème fondamental de l’inférence causale. Ce que nous observons est \(Y_i\) :
\(Y_i = T_iY_i(1) + (1-T_i)Y_i(0)\)
Imaginons qu’on connaisse à la fois \(Y_i(1)\) et \(Y_i(0)\) (ce qui n’est jamais vrai !)
| \(i\) | \(Y_i(1)\) | \(Y_i(0)\) | \(\tau_i\) |
|---|---|---|---|
| Andrei | 1 | 1 | 0 |
| Bamidele | 1 | 0 | 1 |
| Claire | 0 | 0 | 0 |
| Deepal | 0 | 1 | -1 |
Nous avons l’effet du traitement pour chaque individu.
Notez l’hétérogénéité des effets du traitement au niveau individuel.
Mais nous n’observons au maximum qu’un résultat potentiel pour chaque individu, ce qui signifie que nous ne connaissons pas ces effets du traitement.
Effet causal moyen
- Bien que nous ne puissions pas mesurer l’effet causal individuel, \(\tau_i = Y_i(1)-Y_i(0)\), nous pouvons assigner de manière aléatoire des sujets aux conditions de traitement et de contrôle pour estimer l’effet causal moyen, \(\bar{\tau}_i\):
\(\overline{\tau_i} = \frac{1}{N} \sum_{i=1}^N ( Y_i(1)-Y_i(0) ) = \overline{Y_i(1)-Y_i(0)}\)
L’effet causal moyen est également appelé effet moyen du traitement (average treatment effect, ATE).
Plus d’explications sur la randomisation de l’assignation du traitement dans la section suivante.
Paramètres et questions causales
Avant de discuter de la randomisation et de la façon dont elle nous permet d’estimer l’effet causal moyen, sachez que l’effet causal moyen est un type de paramètre.
Un paramètre est une quantité que vous souhaitez connaître (à partir de vos données). C’est la cible de votre recherche que vous avez définie.
Être précis pour votre question de recherche, c’est être précis pour votre paramètre. Pour les questions causales, il s’agit de préciser :
- Le résultat
- Les conditions de traitement et de contrôle
- La population étudiée
D’autres types de paramètres
L’effet causal moyen pour un sous-groupe particulier, i.e. effet causal moyen conditionel (conditional average treatment effect, CATE)
Différences de CATE : différences d’effet moyen du traitement pour un groupe par rapport à un autre groupe.
L’effet moyen du traitement sur les traités (average treatment effect on the treated, ATT)
L’effet moyen local du traitement (local average treatment effect, LATE). “Local” = ceux dont le statut de traitement serait modifié par un encouragement dans une conception incitative (i.e. l’effet causal moyen pour ceux qui se conforment au traitement, complier average causal effect, CACE) ou ceux au voisinage d’un seuil pour une régression sur discontinuité.
Les paramètres sont discutés en détail dans le module paramètres et estimateurs.
Randomisation de l’assignation du traitement
Randomisation de l’assignation du traitement
La randomisation signifie que chaque observation a une probabilité connue d’assignation aux conditions expérimentales entre 0 et 1.
- Aucune unité de l’échantillon expérimental n’est assignée avec certitude au traitement (probabilité = 1) ou au contrôle (probabilité = 0).
Les unités peuvent varier dans leur probabilité d’assignation au traitement.
Par exemple, la probabilité peut varier selon le groupe : les femmes peuvent avoir une probabilité de 25% d’être assignées au traitement tandis que les hommes ont une probabilité différente.
Cela peut même varier d’un individu à l’autre, même si cela compliquerait votre analyse.
Assignation aléatoire vs. échantillonnage aléatoire
Randomisation (du traitement) : assigner des sujets avec une probabilité connue à des conditions expérimentales.
Cette assignation aléatoire du traitement peut être combinée avec tout type d’échantillon (échantillon aléatoire, échantillon de convenance, etc.).
Mais la taille et d’autres caractéristiques de votre échantillon affecteront votre puissance statistique et votre capacité à extrapoler votre découverte à d’autres populations.
Échantillonnage aléatoire (à partir de la population) : sélectionner des sujets dans votre échantillon à partir d’une population avec une probabilité connue.
La randomisation est puissante (1)
Nous cherchons l’ATE, \(\overline{\tau_i}= \overline{Y_i(1)-Y_i(0)}\).
Nous allons utiliser le fait que la moyenne des différences est égale à la différence des moyennes :
ATE \(= \overline{Y_i(1)-Y_i(0)} = \overline{Y_i(1)}-\overline{Y_i(0)}\)
La randomisation est puissante (2)
Assignons de manière aléatoire certaines de nos unités à la condition de traitement. Pour ces unités traitées, nous mesurons le résultat \(Y_i|T_i=1\), qui est le même que \(Y_i(1)\) pour ces unités.
Parce que ces unités ont été assignées de manière aléatoire au traitement, \(Y_i=Y_i(1)\) pour les unités traitées représentent les \(Y_i(1)\) pour toutes nos unités.
En espérance (ou en moyenne sur des expériences répétées (écrit \(E_R[]\))) :
\(E_R[\overline{Y_i}|T_i=1]=\overline{Y_i(1)}\).
\(\overline{Y}|T_i=1\) est un estimateur sans biais de la moyenne des résultats potentiels pour la population sous traitement.
La même logique s’applique pour les unités assignées aléatoirement au contrôle :
\(E_R[\overline{Y_i}|T_i=0]=\overline{Y_i(0)}\).
La randomisation est puissante (3)
- Nous pouvons donc écrire un estimateur pour l’effet moyen du traitement :
\(\hat{\overline{\tau_i}} = ( \overline{Y_i(1)} | T_i = 1 ) - ( \overline{Y_i(0)} | T_i = 0 )\)
- En espérance (ou en moyenne sur des expériences répétées, \(\hat{\overline{\tau_i}}\) égal l’effet moyen du traitement :
\(E_R[Y_i| T_i = 1 ] - E_R[Y_i | T_i = 0] = \overline{Y_i(1)} - \overline{Y_i(0)}\).
- Nous pouvons donc simplement prendre la différence de ces estimateurs sans biais \(\overline{Y_i(1)}\) et \(\overline{Y_i(0)}\) pour obtenir une estimation non biaisée de l’effet moyen du traitement.
Échantillonnage aléatoire
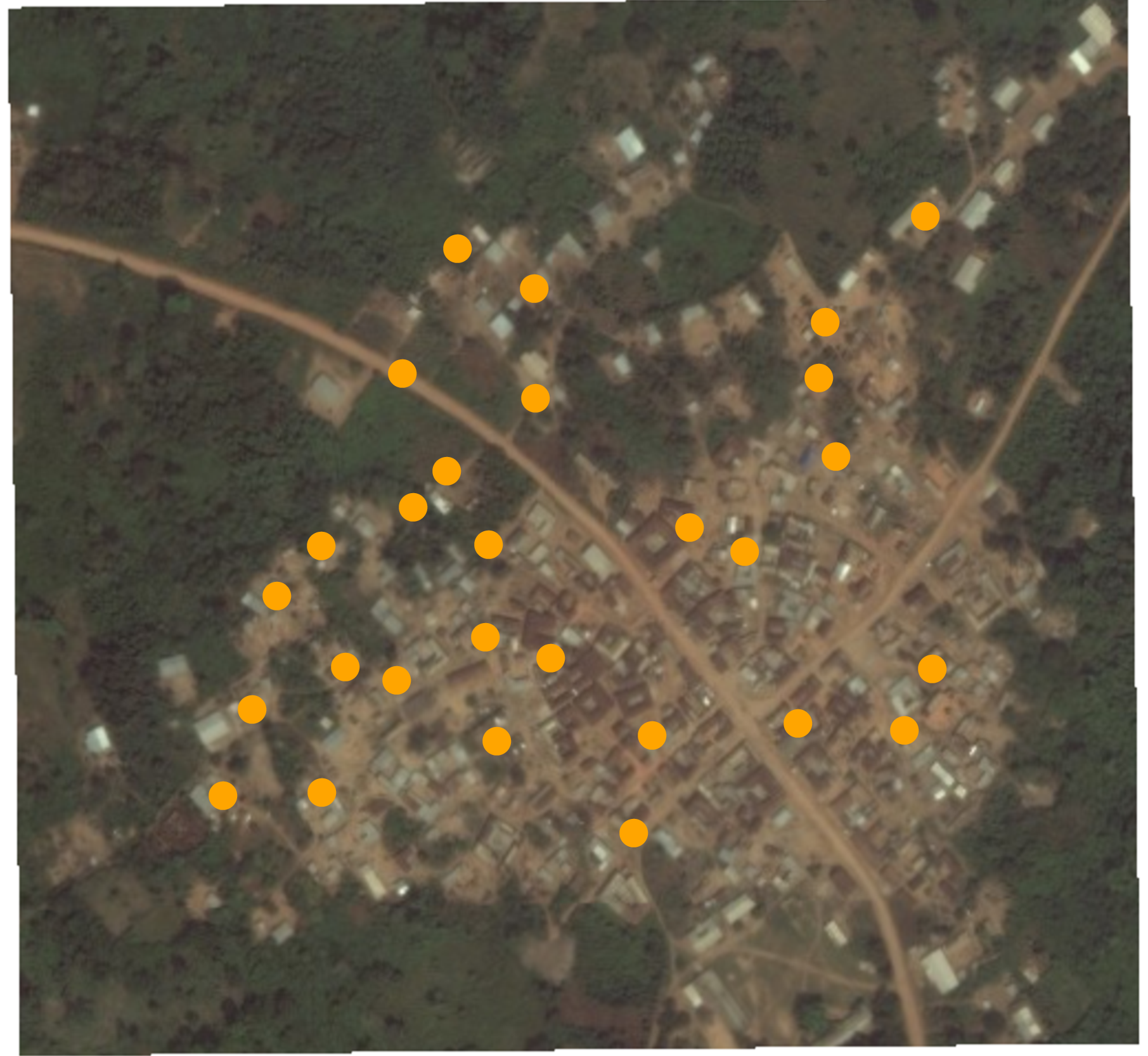
Échantillon aléatoire des foyers
Résultats potentiels
Chaque foyer \(i\) a \(Y_i(1)\) et \(Y_i(0)\).
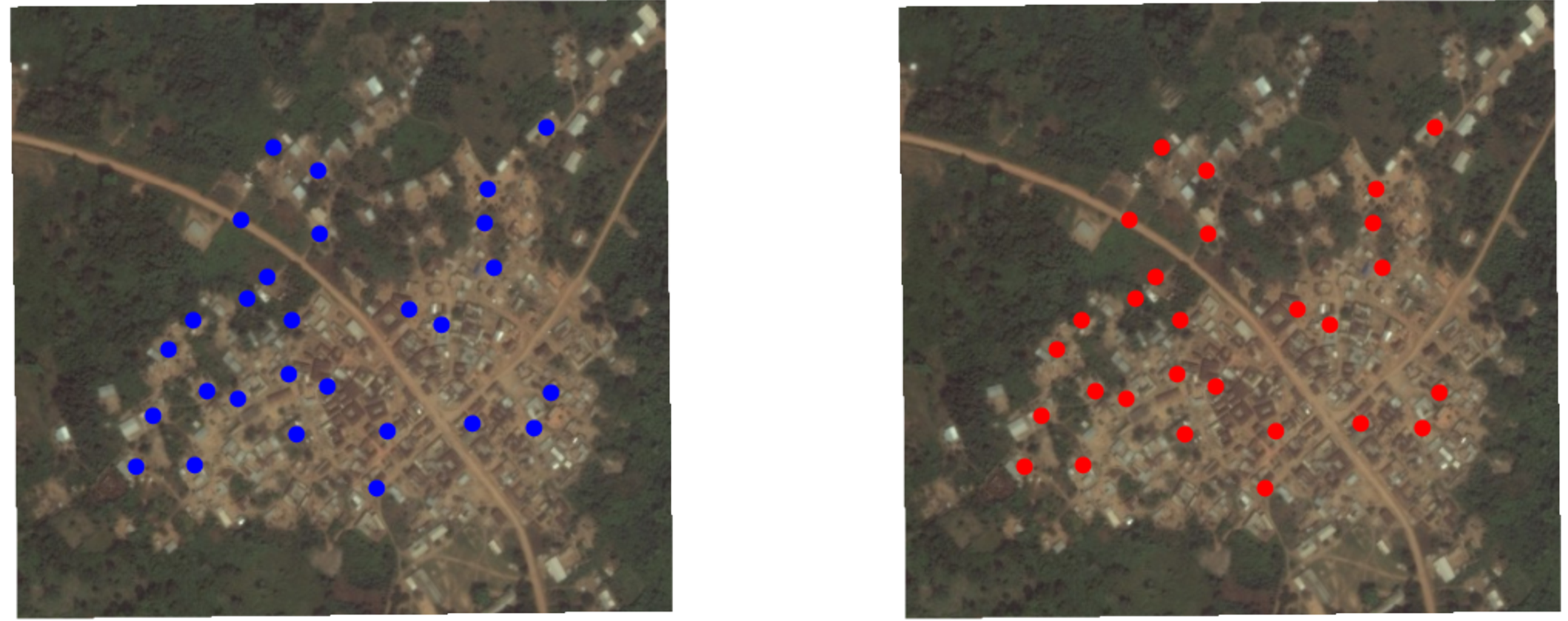
Assignation aléatoire à la condition rouge (1) ou bleue (0)
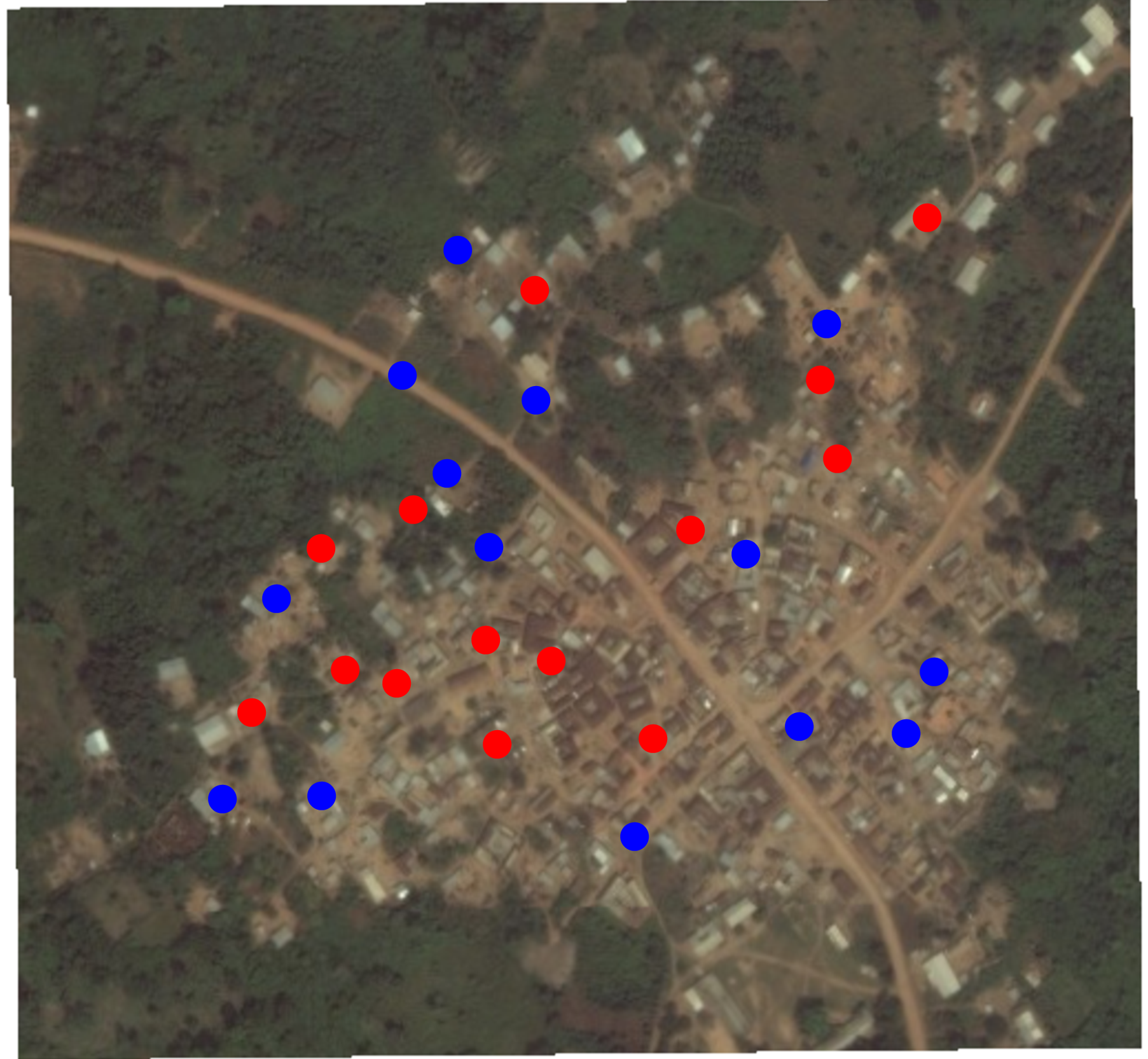
Assignation aléatoire de cet échantillon aléatoire des foyers
Trois hypothèses clés
Pour faire des assertions causales avec une expérience (ou pour juger si nous croyons aux affirmations d’une étude), nous avons besoin de trois hypothèses de base :
Assignation aléatoire des sujets au traitement, ce qui implique que la réception du traitement est statistiquement indépendante des résultats potentiels des sujets.
l’hypothèse SUTVA (Hypothèse stable de la valeur de traitement d’une unité / Stable unit treatment value assumption).
La restriction d’exclusion, i.e. les résultats potentiels d’un sujet ne répondent qu’au traitement défini, et non à d’autres facteurs externes pouvant être corrélés avec le traitement.
Hypothèses clé : SUTVA, partie 1
La non-interférence – Le résultat potentiel d’un sujet reflète uniquement la reception du traitement par ce sujet. Il n’est pas affecté par la façon dont les traitements sont assignés à d’autres sujets.
Une violation classique est le cas des vaccins et de leurs effets de contamination.
Imaginons que je sois dans le groupe de contrôle (pas de vaccin). Le risque de tomber malade (\(Y_i(0)\)) dépend de l’état de traitement des autres personnes (si elles prennent le vaccin ou non), c’est comme si j’avais deux \(Y_i(0)\) différents !
l’hypothèse SUTVA.
Hypothèses clé : SUTVA, partie 2
Pas de variations cachées du traitement
- Disons que le traitement consiste à prendre un vaccin, mais il existe deux types de vaccins et ils ont des compositions différentes.
- Voici un exemple d’infraction : tomber malade lors de la vaccination (\(Y_i(1)\)) est dépendant du vaccin reçu. Nous aurions deux \(Y_i(1)\) différents !
Hypothèses clé : l’exclusion
L’assignation du traitement n’a aucun effet sur les résultats, sauf par l’effet de recevoir ou non le traitement.
Important de définir précisément le traitement.
Important de maintenir la symétrie entre les groupes de traitement et de contrôle (par exemple, en aveugle, en ayant les mêmes procédures de collecte de données pour tous les sujets de l’étude, etc.), afin que l’assignation du traitement n’affecte que le traitement reçu, pas d’autres choses comme les interactions avec les chercheurs que vous ne voulez pas définir dans le cadre du traitement.
La randomisation est puissante (4)
Si l’intervention est aléatoire, alors recevoir ou non l’intervention n’est pas lié aux caractéristiques des bénéficiaires potentiels.
La randomisation fait que ceux qui ont été sélectionnés de manière aléatoire pour ne pas recevoir l’intervention sont de bons remplaçants pour les contrefactuels de ceux qui ont été sélectionnés de manière aléatoire pour recevoir le traitement, et vice versa.
Il faut s’en préoccuper si l’intervention n’était pas aléatoire (= une étude observationnelle).
Études aléatoires vs. observationnelles
Différents types d’études
Études aléatoires
- le traitement est aléatoire, ensuite on mesure les résultats
Études d’observation
- Le traitement n’est pas assigné de manière aléatoire. Il est observé, mais pas manipulé.
Exercice : Apprendre de vos connaissances antérieures
Discutez en petits groupes : concevez le prochain projet pour répondre à l’une de ces questions (ou l’une de vos propres questions causales). Esquissez les caractéristiques clés de deux conceptions — une conception observationnelle et une conception aléatoire.
Exemples de questions de recherche :
Les projets communautaires de reconstruction augmentent-ils la confiance et la coopération au Libéria ? Note d’orientation des politiques publiques EGAP 40
Un suivi par la communauté peut-il augmenter le recours aux cliniques et réduire la mortalité infantile en Ouganda ? Note d’orientation des politiques publiques EGAP 58
Exercice : études observationnelles vs. études aléatoires
Tâches :
Concevez une étude observationnelle idéale (sans randomisation, sans contrôle par les chercheurs mais avec des ressources illimitées pour la collecte des données). Quelles questions poserait un lecteur critique lorsque vos résultats reflètent une relation causale ?
Concevez une étude aléatoire idéale (avec randomisation). Quelles questions poserait un lecteur critique lorsque vos résultats reflètent une relation causale ?
Discussion
Quels sont les éléments clés, les forces et les faiblesses des études aléatoires ?
Quels sont les éléments clés, les forces et les faiblesses des études observationnelles ?
Généralisabilité et validité externe
La randomisation apporte une validité interne élevée à une étude - nous avons appris l’effet causal du traitement sur le résultat avec un certain niveau de confiance.
Mais le résultat d’une étude spécifique à un endroit et moment particuliers peut ne pas être valable dans d’autres contextes (i.e. la validité externe).
C’est une préoccupation générale, pas seulement une préoccupation pour les études aléatoires.
L’initiative Metaketa d’EGAP vise à accumuler des connaissances en pré-planifiant une méta-analyse de plusieurs études qui ont une validité interne élevée en raison de la randomisation.
Comment interpréter “X cause Y” dans cette approche
“X cause Y” n’implique pas nécessairement que W et V ne causent pas Y. X fait partie de l’histoire, mais ce n’est pas toute l’histoire. (Toute l’histoire n’est pas nécessaire pour savoir si X cause Y).
“X cause Y” nécessite un contexte : une allumette provoque une flamme mais cela nécessite de l’oxygène ; les petites salles de classe améliorent les résultats mais nécessitent des enseignants expérimentés et un financement adapté (Cartwright and Hardie 2012).
“X cause Y” peut signifier “Avec X, la probabilité de Y est plus élevée qu’elle ne le serait sans X.” ou “Sans X, il n’y a pas de Y.” Les deux sont compatibles avec l’idée contrefactuelle.