Tests d’hypothèses: résumer les informations sur les effets causaux
Mettre votre nom
04-03-2022
- Le rôle des tests d’hypothèses dans l’inférence causale
- Les bases du test
d’hypothèse
- Ingrédients d’un test d’hypothèse
- Une hypothèse est l’énoncé ou le modèle d’une relation entre des résultats potentiels
- Les statistiques de test résument les relations entre le traitement et les résultats
- La conception lie la statistique de test et l’hypothèse
- La conception guide la création d’une distribution de statistiques de test hypothétiques
- Courbe des distributions de randomisation sous l’hypothèse nulle
- Les \(p\)-valeurs résument les graphiques
- Comment faire cela en R : COIN
- Comment faire cela en R : RItools
- Comment faire cela en R : RI2
- Sujets suivants
- Tester l’hypothèse nulle faible
- Rejeter l’hypothèse nulle
- Rejeter l’hypothèse nulle et faire des erreurs
- Taux de faux positifs dans les tests d’hypothèses
- Erreurs de faux positifs et de faux négatifs
- Un test unique d’une seule hypothèse
- Les décisions impliquent des erreurs
- Diagnostiquer les taux de faux positifs par simulation
- Diagnostiquer les taux de faux positifs par simulation
- Diagnostiquer les taux de faux positifs par simulation
- Diagnostiquer les taux de faux positifs par simulation
- Diagnostiquer les taux de faux positifs par simulation
- Taux de faux positifs avec \(N=60\) et résultat binaire
- Taux de faux positifs avec \(N=60\) et résultat continu
- Sommaire
- Approfondissement
- Tester de nombreuses
hypothèses
- Quand pouvons-nous tester de nombreuses hypothèses ?
- Taux de faux positifs dans les tests d’hypothèses multiples
- Découvertes avec tests multiples
- Deux taux d’erreur principaux à contrôler lors du test de nombreuses hypothèses
- Questions à résultats multiples
- Tests d’hypothèses multiples : résultats multiples
- Pouvons-nous
détecter un effet sur le résultat
Y1? - Pour lequel des cinq résultats pouvons-nous détecter un effet ?
- Pouvons-nous détecter un effet pour un des cinq résultats ?
- Comparaison des approches I
- Comparaison des approches II
- La correction de Holm
- Approches pour tester des hypothèses avec plusieurs bras
- Tests d’hypothèses multiples : bras de traitement multiples
- Tests d’hypothèses multiples : bras de traitement multiples
- Tests d’hypothèses multiples : bras de traitement multiples
- Résumé
- Références
Le rôle des tests d’hypothèses dans l’inférence causale
Points principaux
L’inférence statistique (e.g., les tests d’hypothèses et les intervalles de confiance) nécessite l’inférence — i.e. raisonner sur ce qui n’a pas été observé.
Les \(p\)-valeurs nécessitent des distributions de probabilité.
Une randomisation (ou une conception) + une hypothèse + une fonction de test statistique \(\rightarrow\) distributions de probabilité représentant l’hypothèse (distributions de référence)
Valeurs observées des tests statistiques + distribution de référence \(\rightarrow\) \(p\)-valeur.
Le role des tests d’hypothèses dans l’inférence causale I
Le problème fondamental de l’inférence causale dit que nous ne pouvons voir qu’un seul résultat potentiel pour une unité donnée.
Donc, si un effet causal contrefactuel du traitement, \(T\), pour Jake se produit lorsque \(y_{\text{Jake},T=1} \ne y_{\text{Jake},T=0}\), alors comment pouvons-nous en savoir plus sur l’effet causal ?
Une solution est l’estimation des moyennes des effets causaux (les ATE, ITT, LATE).
C’est ce que nous appellons l’approche de Neyman.
Le role des tests d’hypothèses dans l’inférence causale II
Une autre solution consiste à faire des affirmations ou des suppositions sur les effets causaux.
On pourrait dire : “Je pense que l’effet sur Jake est de 5”. ou “Cette expérience n’a eu d’effet sur personne.” Et puis nous demandons “Quelles preuves apporte cette expérience à propos de cette affirmation ?”
Cette preuve est contenue dans la \(p\)-valeur.
C’est ce que nous appelons l’approche de Fisher.
Le role des tests d’hypothèses dans l’inférence causale III
L’approche du test d’hypothèse pour l’inférence causale ne fournit pas une meilleure supposition, mais indique la quantité d’informations que la conception de recherche fournit pour cette assertion causale.
L’approche par estimation fournit une meilleure supposition, mais ne vous dit pas ce que vous savez sur cette supposition.
- Par exemple, une supposition avec \(N=10\) semble en dire moins sur l’effet que pour \(N=1000\).
- Par exemple, une supposition avec 95% de \(Y=1\) et 5% de \(Y=0\) semble en dire moins que lorsque les résultats sont répartis également entre 0 et 1.
Nous rapportons presque toujours les deux approches, car les deux nous aident à prendre des décisions : “Notre supposition de l’effet du traitement était de 5, et nous pouvions rejeter l’idée que l’effet était de 0 (\(p\)=0,01).”
Les bases du test d’hypothèse
Ingrédients d’un test d’hypothèse
Une hypothèse est un énoncé concernant une relation entre les résultats potentiels.
Une statistique de test résume la relation entre le traitement et les résultats observés.
La conception permet de lier l’hypothèse et la statistique de test : calculez une statistique de test qui décrit une relation entre des résultats potentiels.
La conception indique aussi comment générer une distribution des statistiques de test possibles implicitement liés à l’hypothèse.
Une \(p\)-valeur décrit la relation entre notre statistique de test observée et la distribution de possibles statistiques de test.
Une hypothèse est l’énoncé ou le modèle d’une relation entre des résultats potentiels
| Résultat | Traitement | \(y_{i,0}\) | ITE | \(y_{i,1}\) | \(Y>0\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 10 | 10 | 0 |
| 30 | 1 | 0 | 30 | 30 | 0 |
| 0 | 0 | 0 | 200 | 200 | 0 |
| 1 | 0 | 1 | 90 | 91 | 0 |
| 11 | 1 | 1 | 10 | 11 | 0 |
| 23 | 1 | 3 | 20 | 23 | 0 |
| 34 | 1 | 4 | 30 | 34 | 0 |
| 45 | 1 | 5 | 40 | 45 | 0 |
| 190 | 0 | 190 | 90 | 280 | 1 |
| 200 | 0 | 200 | 20 | 220 | 1 |
Par exemple, l’hypothèse nulle stricte d’absence d’effet est \(H_0 : y_{i,1} = y_{i,0}\)
Les statistiques de test résument les relations entre le traitement et les résultats
## La statistique de test de la différence des moyennes
meanTT <- function(ys, z) {
mean(ys[z == 1]) - mean(ys[z == 0])
}
## La statistique de test de la différence des moyennes selon le rang
meanrankTT <- function(ys, z) {
ranky <- rank(ys)
mean(ranky[z == 1]) - mean(ranky[z == 0])
}
observedMeanTT <- meanTT(ys = Y, z = T)
observedMeanRankTT <- meanrankTT(ys = Y, z = T)
observedMeanTT[1] -49.6[1] 1La conception lie la statistique de test et l’hypothèse
Ce que nous observons pour chaque personne \(i\) (\(Y_i\)) est soit ce que nous aurions observé en traitement (\(y_{i,1}\)) ou ce que nous aurions observé en contrôle (\(y_{i ,0}\)).
\[Y_i = T_i y_{i,1} + (1-T_i)* y_{i,0}\]
Donc, si \(y_{i,1}=y_{i,0}\) alors \(Y_i = y_{i,0}\).
Ce que nous observons réellement est ce que nous aurions observé dans la condition de contrôle.
La conception guide la création d’une distribution de statistiques de test hypothétiques
Nous devons savoir comment répéter notre expérience:
Ensuite, on répète notre expérience en calculant à chaque fois une nouvelle statistique de test donnée par l’hypothèse et la conception :
Courbe des distributions de randomisation sous l’hypothèse nulle
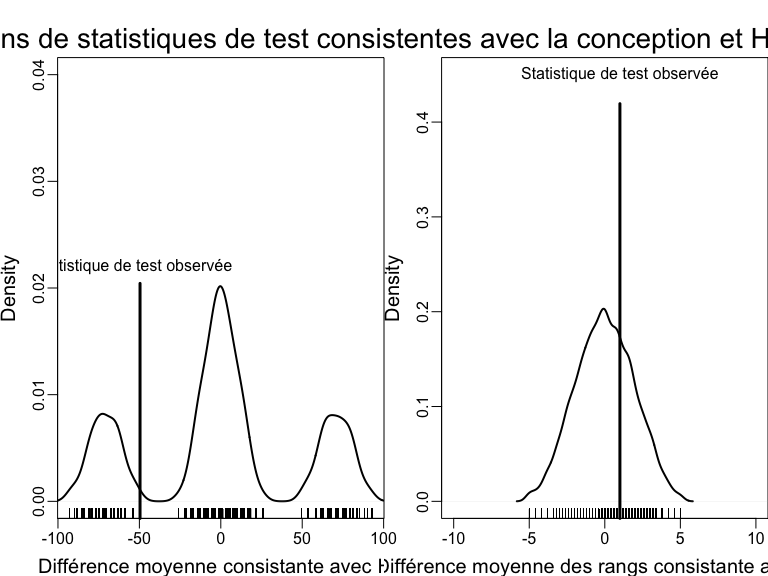
Utiliser la conception d’expérience pour tester une hypothèse avec deux statistiques de test différentes.
Les \(p\)-valeurs résument les graphiques
Comment devrions-nous interpréter ces \(p\)-valeurs ? (Notez qu’elles sont unilatérales)
pMeanTT <- mean(possibleMeanDiffsH0 >= observedMeanTT)
pMeanRankTT <- mean(possibleMeanRankDiffsH0 >= observedMeanRankTT)
pMeanTT[1] 0.7785[1] 0.3198Comment faire cela en R : RItools
Installez d’abord une version de développement du package RItools
# dev_mode() ## dont install the package globally
renv::install("markmfredrickson/RItools@randomization-distribution",
force = TRUE
)
# dev_mode()Utilisez ensuite la fonction RItest.
# dev_mode()
library(RItools)
thedesignA <- simpleRandomSampler(total = N, z = dat$T, b = rep(1, N))
pMean4 <- RItest(
y = dat$Y, z = dat$T, samples = 1000, test.stat = meanTT,
sampler = thedesignA
)
pMeanRank4 <- RItest(
y = dat$Y, z = dat$T, samples = 1000, test.stat = meanrankTT,
sampler = thedesignA
)
pMean4
pMeanRank4
# dev_mode() ## et désactiver le dev_modepMean4
Call: RItest(y = dat$Y, z = dat$T, test.stat = meanTT, sampler = thedesignA,
samples = 1000)
Value Pr(>x)
Statistique de test observée -49.6 0.78
pMeanRank4
Call: RItest(y = dat$Y, z = dat$T, test.stat = meanrankTT, sampler = thedesignA,
samples = 1000)
Value Pr(>x)
Statistique de test observée 1 0.32Comment faire cela en R : RI2
Comment interpréter la \(p\)-valeur bilatérale ici ?
## en utilisant le package ri2
library(ri2)
thedesign <- declare_ra(N = N)
dat$Z <- dat$T
pMean4 <- conduct_ri(Y ~ Z,
declaration = thedesign,
sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMean4) term estimate two_tailed_p_value
1 Z -49.6 0.4444pMeanRank4 <- conduct_ri(rankY ~ Z,
declaration = thedesign,
sharp_hypothesis = 0, data = dat, sims = 1000
)
summary(pMeanRank4) term estimate two_tailed_p_value
1 Z 1 0.6349Sujets suivants
Tester l’hypothèse nulle faible, \(H_0 : \bar{y}_{1} = \bar{y}_{0}\).
Rejeter l’hypothèse nulle (et faire des erreurs de faux positifs et/ou de faux négatifs).
Conserver un taux d’erreur correct de faux positifs quand on teste plus d’une hypothèse.
Puissance statistique des tests d’hypothèses (Module sur la puissance statistique et les diagnostics de conception).
Tester l’hypothèse nulle faible
Tester l’hypothèse nulle faible d’absence d’effets moyens
L’hypothèse nulle faible est une affirmation sur les agrégats. Elle est presque toujours exprimée en termes de moyennes : \(H_0 : \bar{y}_{1} = \bar{y}_{0}\)
La statistique de test pour cette hypothèse est presque toujours la simple différence des moyennes (c’est-à-dire
meanTT()ci-dessus).
lm1 <- lm(Y ~ T, data = dat)
lm1P <- summary(lm1)$coef["T", "Pr(>|t|)"]
ttestP1 <- t.test(Y ~ T, data = dat)$p.value
library(estimatr)
ttestP2 <- difference_in_means(Y ~ T, data = dat)
c(lm1P = lm1P, ttestP1 = ttestP1, tttestP2 = ttestP2$p.value) lm1P ttestP1 tttestP2.T
0.3321 0.3587 0.3587 - Pourquoi la \(p\)-valeur pour les moindres carrés ordinaires est différente ? Quelles hypothèses utiliser pour la calculer ?
Tester l’hypothèse nulle faible d’absence d’effets moyens
La variation et l’emplacement de \(Y\) changent avec le traitement dans cette simulation.
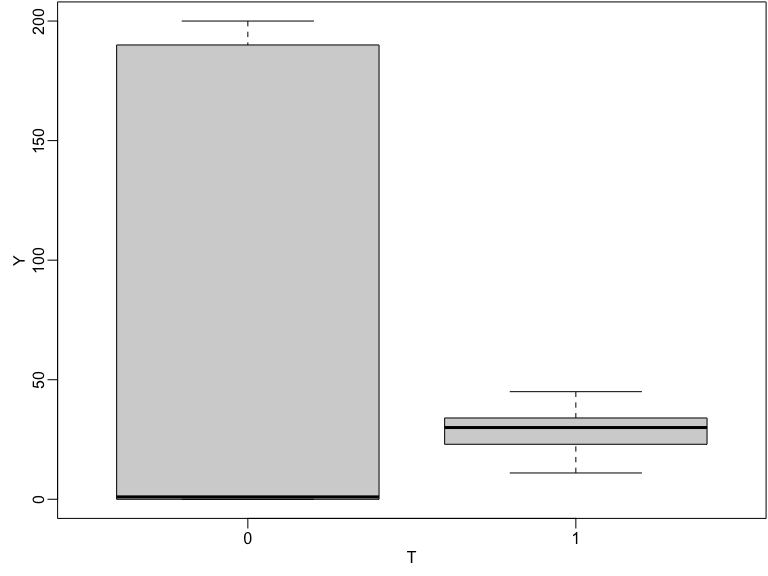
Résultats observés en fonction du statut de traitement
Tester l’hypothèse nulle faible d’absence d’effets moyens
## à la main:
varEstATE <- function(Y, T) {
var(Y[T == 1]) / sum(T) + var(Y[T == 0]) / sum(1 - T)
}
seEstATE <- sqrt(varEstATE(dat$Y, dat$T))
obsTStat <- observedMeanTT / seEstATE
c(
observedTestStat = observedMeanTT,
stderror = seEstATE,
tstat = obsTStat,
pval = 2 * min(
pt(obsTStat, df = 8, lower.tail = TRUE),
pt(obsTStat, df = 8, lower.tail = FALSE)
)
)observedTestStat stderror tstat pval
-49.6000 48.0448 -1.0324 0.3321 Rejeter l’hypothèse nulle
Rejeter l’hypothèse nulle et faire des erreurs
“Typiquement, le niveau du test [\(\alpha\)] est une promesse sur la performance du test et la taille est un fait sur sa performance…” (Rosenbaum 2010, Glossaire)
\(\alpha\) est la probabilité de rejeter l’hypothèse nulle lorsque l’hypothèse nulle est vraie.
Comment doit-on interpréter \(p\)=0.78 ? Qu’en est-il de \(p\)=0.32 (nos tests pour l’hypothèse nulle stricte) ?
Que signifie “rejeter” \(H_0 : y_{i,1}=y_{i,2}\) à \(\alpha=0,05\) ?
Taux de faux positifs dans les tests d’hypothèses
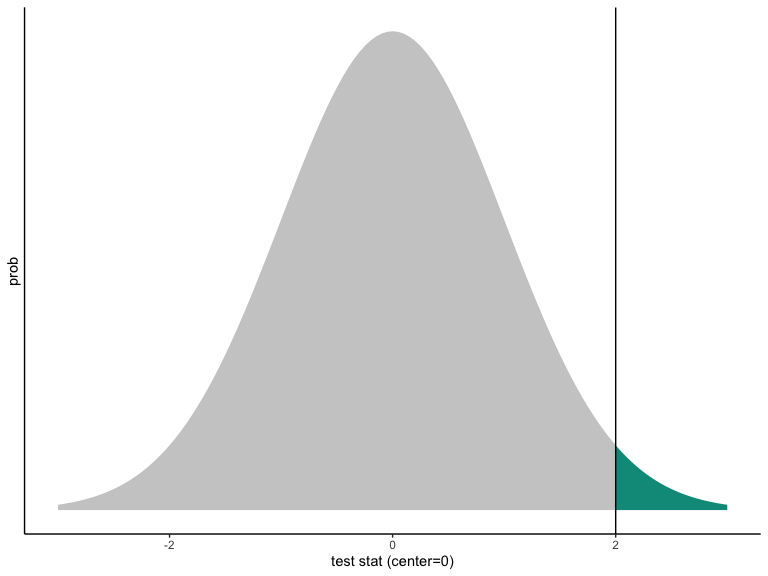
P-valeur unilatérale d’une statistique de test normale.
Attention:
La courbe est centrée sur la valeur hypothétique.
La courbe représente le monde de l’hypothèse.
La \(p\)-valeur décrit à quel point il serait rare de voir la statistique de test observée (ou une valeur plus éloignée de la valeur hypothétique) dans le monde de l’hypothèse nulle.
Sur la figure, la valeur observée de la statistique de test est cohérente avec la distribution hypothétique, mais pas très cohérente.
Même si \(p < 0,05\) (ou \(p < 0,001\)) la statistique de test observée doit refléter en partie la distribution hypothétique. Cela signifie que vous pouvez toujours faire une erreur lorsque vous rejetez une hypothèse nulle.
Erreurs de faux positifs et de faux négatifs
Si nous disons, “le résultat expérimental est significativement différent de la valeur hypothétique de zéro (\(p=0,001\)) ! Nous rejetons cette hypothèse !” lorsque la vérité est zéro nous faisons une erreur de faux positifs (prétendant détecter quelque chose lorsqu’il n’y a pas de signal, seulement du bruit).
Si nous disons : “Nous ne pouvons pas distinguer ce résultat de zéro (\(p=0,3\)). Nous ne pouvons pas rejeter l’hypothèse de zéro.” lorsque la vérité n’est pas zéro nous faisons une erreur de faux négatifs (prétendant l’incapacité à détecter quelque chose lorsqu’il y a un signal, mais qu’il est noyé dans le bruit).
Un test unique d’une seule hypothèse
Un test unique d’une seule hypothèse devrait rarement augmenter le taux de faux positifs (par exemple, si nous définissons \(\alpha=0,05\)) alors nous acceptons que notre procédure de test produise des faux positifs dans au plus de 5% des tests d’une assignation de traitement donnée dans une expérience donnée.
De plus, un test unique d’une seule hypothèse doit détecter le signal lorsqu’il existe — il doit avoir une puissance statistique élevée. En d’autres termes, il ne doit pas manquer la détection du signal lorsqu’il existe (c’est-à-dire qu’il devrait avoir un faible taux de faux négatifs).
Les décisions impliquent des erreurs
Si les erreurs sont nécessaires, comment les diagnostiquer ? Comment savoir si notre procédure de tests d’hypothèses génère trop de faux positifs ?
Diagnostiquez par simulation !
Diagnostiquer les taux de faux positifs par simulation
A travers les répétitions de la conception :
- Créer une hypothèse nulle vraie.
- Testez cette hypothèse.
- La \(p\)-valeur doit être élevée si le test fonctionne correctement.
La proportion de petites \(p\)-valeurs ne doit pas dépasser \(\alpha\) si le test fonctionne correctement.
Diagnostiquer les taux de faux positifs par simulation
Ex: avec un résultat binaire. Le test fonctionne-t-il comme il se doit ? À quoi ressemblent les p-valeurs lorsqu’il n’y a pas d’effet ?
collectPValues <- function(y, trt, thedistribution = exact()) {
## Faire en sorte que Y et T n'aient aucune relation en randomisant T à nouveau
new_trt <- repeatExperiment(length(y))
thedata <- data.frame(new_trt = new_trt, y = y)
thedata$ranky <- rank(y)
thedata$new_trtF <- factor(thedata$new_trt)
## Les 4 tests
thelm <- lm(y ~ new_trt, data = thedata)
t_test_CLT <- difference_in_means(y ~ new_trt, data = thedata)
t_test_exact <- oneway_test(y ~ new_trtF,
data = thedata,
distribution = thedistribution
)
t_test_rank_exact <- oneway_test(ranky ~ new_trtF,
data = thedata,
distribution = thedistribution
)
owP <- coin::pvalue(t_test_exact)[[1]]
owRankP <- coin::pvalue(t_test_rank_exact)[[1]]
## Renvoyer les p-valeurs
return(c(
lmp = summary(thelm)$coef["new_trt", "Pr(>|t|)"],
neyp = t_test_CLT$p.value[[1]],
rtp = owP,
rtpRank = owRankP
))
}Diagnostiquer les taux de faux positifs par simulation
Lorsqu’il n’y a pas d’effet, un test de l’hypothèse nulle d’absence d’effet doit produire une grande p-valeur.
Si le test fonctionne bien, nous devrions voir principalement de grandes p-valeurs et très peu de petites p-valeurs.
Quelques-unes des p-valeurs pour les quatre tests différents (nous avons fait 5000 simulations, en voici 5)
[,1] [,2] [,3] [,4] [,5]
lmp 1 1 1 1 0.1411
neyp 1 1 1 1 0.1778
rtp 1 1 1 1 0.4444
rtpRank 1 1 1 1 0.4444Diagnostiquer les taux de faux positifs par simulation
En fait, s’il n’y a pas d’effet, et si nous décidons de rejeter l’hypothèse nulle d’absence d’effet avec \(\alpha=0,25\), nous ne voudrions pas plus de 25% des p-valeurs de cette simulation en dessous de p=0,25. Que voit-on ici ? Quels tests semblent avoir des taux de faux positifs trop élevés ?
## Calculer la proportion de p-valeurs inférieures à 0,25
## pour chaque ligne de pDist
apply(pDist, 1, function(x) {
mean(x < .25)
}) lmp neyp rtp rtpRank
0.4536 0.4536 0.0000 0.0000 Diagnostiquer les taux de faux positifs par simulation
Comparez les tests en traçant la proportion de p-valeurs inférieures à un nombre donné. Les tests “d’inférence de randomisation” contrôlent le taux de faux positifs (ce sont les tests avec permutation directe répétant l’expérience).
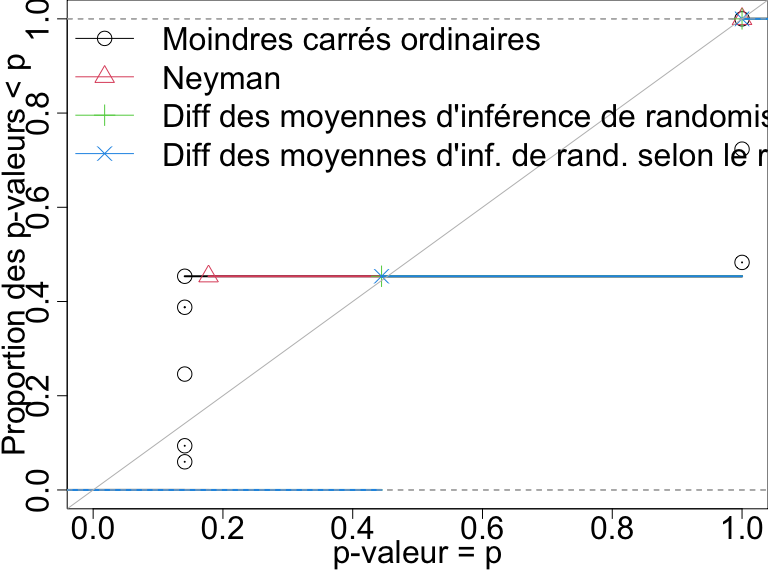
Distributions des p-valeurs quand il n y a aucun effet pour quatre tests avec n=10. Un test qui contrôle son taux de faux positifs doit avoir des points sur ou en dessous de la ligne diagonale.
Taux de faux positifs avec \(N=60\) et résultat binaire
Dans cette conception, seuls les tests basés sur l’inférence de randomisation directe contrôlent le taux de faux positifs.
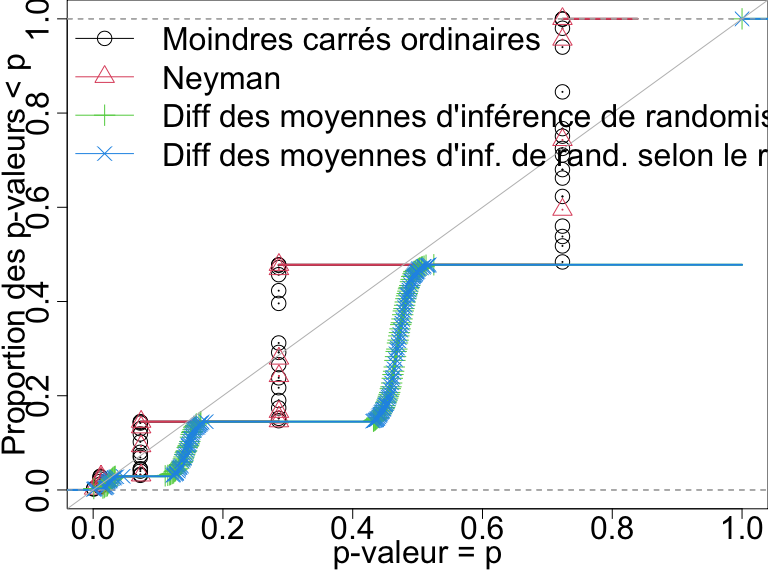
Distributions des p-valeurs quand il n y a aucun effet pour quatre tests avec n=60 et un résultat binaire. Un test qui contrôle son taux de faux positifs doit avoir des points sur ou en dessous de la ligne diagonale.
Taux de faux positifs avec \(N=60\) et résultat continu
Ici, tous les tests contrôlent bien le taux de faux positifs.
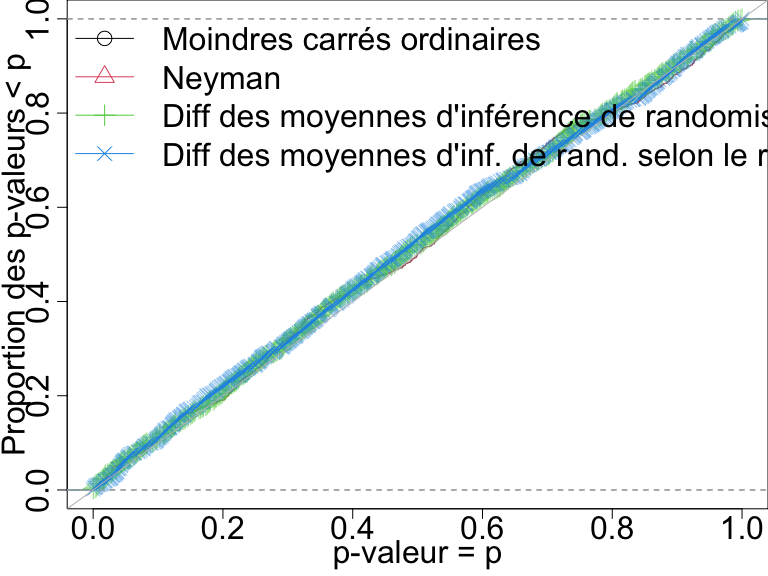
Distributions des p-valeurs quand il n y a aucun effet pour quatre tests avec n=60 et un résultat continu. Un test qui contrôle son taux de faux positifs doit avoir des points sur ou en dessous de la ligne diagonale.
Sommaire
Un bon test :
met rarement en doute la vérité, et
distingue facilement le signal du bruit (met souvent en doute les contrevérités).
Nous pouvons savoir si notre procédure de test contrôle le taux de faux positifs compte tenu de notre dsign.
Lorsque le taux de faux positifs n’est pas contrôlé, qu’est-ce qui ne va pas ? (probablement lié à l’asymptotique).
Approfondissement
Quelques sujets approfondis liés aux tests d’hypothèses
Même si une procédure de test donnée contrôle le taux de faux positifs pour un seul test, elle peut ne pas contrôler le taux pour un groupe de tests. Voir 10 choses à savoir sur les comparaisons multiples pour les approches de contrôle de taux de rejet dans plusieurs tests.
Un intervalle de confiance de \(100(1-\alpha)\)% peut être défini comme la plage d’hypothèses où toutes les \(p\)-valeurs sont supérieures ou égales à \(\alpha\). C’est ce qu’on appelle l’inversion du test d’hypothèse (Rosenbaum (2010)). Autrement dit, un intervalle de confiance est un ensemble de tests d’hypothèses.
Que savoir de plus sur les tests d’hypothèses
Une estimation ponctuelle basée sur des tests d’hypothèse est appelée une estimation ponctuelle de Hodges-Lehmann (Rosenbaum (1993),Hodges and Lehmann (1963)).
Un ensemble de tests d’hypothèses peut être combiné en un seul test d’hypothèse (Hansen and Bowers (2008),Caughey, Dafoe, and Seawright (2017)).
Dans les tests d’équivalence, on peut émettre l’hypothèse que deux statistiques de test sont équivalentes (c’est-à-dire que le groupe de traitement est le même que le groupe témoin) plutôt que d’environ une seule statistique de test (la différence entre les deux groupes est de zéro) (Hartman and Hidalgo (2018)).
Étant donné qu’un test d’hypothèse est un modèle de résultats potentiels, on peut utiliser les tests d’hypothèses pour en savoir plus sur des modèles complexes, tels que des modèles de contamination et de propagation des effets de traitement à travers les réseaux (Bowers, Fredrickson, and Panagopoulos (2013), Bowers, Fredrickson, and Aronow (2016), Bowers et al. (2018))
Exercice : Tests d’hypothèses et statistiques de test
Si une intervention était très efficace pour augmenter la variabilité d’un résultat mais ne changeait pas la moyenne, la \(p\)-valeur rapportée par R ou Stata en utilisant
lm_robust()oudifference_of_means()ouregout.testserait-elle grande ou petite ?Si une intervention réduisait modérément la moyenne dans le groupe témoin mais augmentait considérablement quelques résultats (comme un effet 10 fois supérieur), la \(p\)-valeur de R
lm_robust()oudifference_of_means()serait-elle grande ou petite ?
Tester de nombreuses hypothèses
Quand pouvons-nous tester de nombreuses hypothèses ?
L’effet d’un traitement expérimental diffère-t-il entre les différents groupes ? Les différences de l’effet du traitement pourraient-elles survenir en raison de certaines caractéristiques de base des sujets expérimentaux ?
Parmi plusieurs stratégies de communication, lesquelles ont été les plus efficaces sur un résultat particulier ?
Parmi plusieurs résultats, lesquels ont été influencés par une seule intervention expérimentale ?
Taux de faux positifs dans les tests d’hypothèses multiples
Supposons que notre probabilité de faux positifs est de 0,05 pour un seul test. Que se passe-t-il si nous demandons: (1) lequel de ces 10 résultats a une relation statistiquement significative avec les deux bras de traitement ? (2) lequel de ces 10 bras de traitement avait une relation statistiquement significative avec un résultat unique ?
- La probabilité de faux positifs doit être inférieure ou égale à 0,05 dans un test.
- La probabilité de faux positifs doit être inférieure ou égale à \(1 - ( ( 1 - 0,05 ) \times (1 - 0,05) ) = 0,0975\) dans 2 tests.
- La probabilité d’avoir au moins un faux positif avec \(\alpha=0,05\) dans 10 tests devrait être \(\le\) \(1 - (1-0,05)^{10}=0,40\).
Découvertes avec tests multiples
Nombre d’erreurs commises en testant \(m\) hypothèses nulles (Table 1 de Benjamini and Hochberg 1995). Les cellules sont le nombre de tests. \(R\) est le nombre de “découvertes” et \(V\) est le nombre de fausses découvertes, \(U\) est le nombre de non-rejets corrects et \(S\) est le nombre de rejets corrects.
| Déclarés Non-Significatifs | Déclarés Significatifs | Total | |
|---|---|---|---|
| hypo. nulle vraie (\(H_{true}=0\)) | |
|
\(m_0\) |
| hypo. nulle fausse (\(H_{true} \ne 0\)) | |
|
m - \(m_0\) |
| Total | |
|
m |
Deux taux d’erreur principaux à contrôler lors du test de nombreuses hypothèses
Le taux d’erreur par famille (family wise error rate, FWER) est de \(P(V>0)\) (Probabilité d’un quelconque de faux positif).
à contrôler si nous prévoyons de prendre une décision sur les résultats de nos multiples tests. Le projet de recherche est essentiellement confirmatoire.
voir par exemple les projets de l’OES : les agences fédérales prennent des décisions sur leurs programmes en fonction des résultats détectés (ou non).
Le taux de fausse découverte (false discovery rate, FDR) est de \(E(V/R | R>0)\) (proportion moyenne de faux positifs compte tenu de certains rejets).
à contrôler si nous utilisons cette expérience pour planifier la prochaine expérience. Nous sommes prêts à accepter une probabilité d’erreur plus élevée dans le but de nous donner plus de possibilités de découverte.
par exemple, on pourrait imaginer une organisation, un gouvernement ou une ONG qui déciderait de mener une série d’expériences dans le cadre d’un programme exploratoire : aucune expérience ne détermine seule la prise de décision, cela offre plus de possibilité pour l’exploration.
Nous nous concentrerons sur le FWER mais recommandons de penser au FDR pour les programmes exploratoires.
Questions à résultats multiples
Quel est l’effet d’un traitement sur plusieurs résultats ?
Sur quels résultats le traitement a-t-il eu un effet (parmi l’ensemble des résultats) ?
La deuxième question, en particulier, peut conduire aux problèmes de taux d’erreur non contrôlés par famille (voir ci-dessus).
Tests d’hypothèses multiples : résultats multiples
Imaginez que nous ayons cinq résultats et un traitement (ici les résultats potentiels et observés) :
ID T Y1_T_0 Y1_T_1 Y2_T_0 Y2_T_1 Y3_T_0 Y3_T_1 Y4_T_0 Y4_T_1 Y5_T_0 Y5_T_1
1 001 0 0.19 0.19 0.366 0.366 0.546 0.546 -0.626 -0.626 -0.125 -0.125
2 002 0 -0.43 -0.43 0.931 0.931 -2.233 -2.233 1.309 1.309 1.078 1.078
3 003 0 0.91 0.91 -1.907 -1.907 0.288 0.288 -0.133 -0.133 -1.261 -1.261
4 004 0 1.79 1.79 0.052 0.052 0.544 0.544 -1.608 -1.608 -0.452 -0.452
5 005 1 1.00 1.00 -0.848 -0.848 -1.192 -1.192 -1.308 -1.308 -1.027 -1.027
6 006 0 1.11 1.11 -0.368 -0.368 -0.018 -0.018 -0.045 -0.045 0.068 0.068 ID T Y1 Y2 Y3 Y4 Y5
1 001 0 0.19 0.366 0.546 -0.626 -0.125
2 002 0 -0.43 0.931 -2.233 1.309 1.078
3 003 0 0.91 -1.907 0.288 -0.133 -1.261
4 004 0 1.79 0.052 0.544 -1.608 -0.452
5 005 1 1.00 -0.848 -1.192 -1.308 -1.027
6 006 0 1.11 -0.368 -0.018 -0.045 0.068Pouvons-nous détecter un effet sur le résultat Y1
?
Pouvons-nous détecter un effet sur le résultat Y1 ?
(c’est-à-dire, le test d’hypothèse produit-il une \(p\)-valeur suffisamment petite ?)
[1] 0.88## Notez que la p-valeur du test t est également un test du chi carré
coin::pvalue(independence_test(Y1 ~ factor(T),
data = dat1,
teststat = "quadratic"
))[1] 0.88Pour lequel des cinq résultats pouvons-nous détecter un effet ?
Pour lequel des cinq résultats pouvons-nous détecter un effet ? (c’est-à-dire, l’un des cinq tests d’hypothèses produit-il une \(p\)-valeur suffisamment petite ?)
p1 <- coin::pvalue(oneway_test(Y1 ~ factor(T), data = dat1))
p2 <- coin::pvalue(oneway_test(Y2 ~ factor(T), data = dat1))
p3 <- coin::pvalue(oneway_test(Y3 ~ factor(T), data = dat1))
p4 <- coin::pvalue(oneway_test(Y4 ~ factor(T), data = dat1))
p5 <- coin::pvalue(oneway_test(Y5 ~ factor(T), data = dat1))
theps <- c(p1 = p1, p2 = p2, p3 = p3, p4 = p4, p5 = p5)
sort(theps) p5 p4 p3 p2 p1
0.27 0.30 0.43 0.59 0.88 Pouvons-nous détecter un effet pour un des cinq résultats ?
Pouvons-nous détecter un effet pour un des cinq résultats ? (c’est-à-dire, un test d’hypothèse pour tous les résultats ensemble produit-il une \(p\)-valeur suffisamment petite ?)
coin::pvalue(independence_test(Y1 + Y2 + Y3 + Y4 + Y5 ~ factor(T),
data = dat1, teststat = "quadratic"
))[1] 0.67Quelle approche est susceptible de nous induire en erreur avec trop de résultats “statistiquement significatifs” (5 tests ou 1 test omnibus) ?
Comparaison des approches I
Faisons une simulation pour en savoir plus sur ces approches de test.
Nous allons (1) définir les véritables effets causaux à 0, (2) réassigner le traitement à plusieurs reprises, et (3) à chaque fois, faire chacun de ces trois tests.
Puisque le véritable effet est 0, nous nous attendons à ce que la plupart des \(p\)-valeurs soient grandes. (En fait, nous ne voulons pas plus de 5% des \(p\)-valeurs supérieures à \(p=0,05\) si nous utilisons le critère d’acceptance ou de rejet \(\alpha=0,05\)).
Comparaison des approches II
| estimator | fwer |
|---|---|
| test-t omnibus | 0.04 |
| test-t pour tous | 0.22 |
| test-t pour tous holm adj | 0.04 |
| test-t pour Y1 | 0.05 |
L’approche utilisant 5 tests produit une \(p\)-valeur \(< 0,05\) beaucoup trop souvent — rappelons qu’il n’y a aucun effet causal pour aucun de ces résultats.
Un test d’un seul résultat (ici
Y1) une \(p\)-valeur \(< 0,05\) pour moins de 5% des simulations.Le test omnibus montre également un taux d’erreur bien maîtrisé.
L’utilisation d’une correction de tests multiples (ici nous utilisons la correction de Holm) contrôle également correctement le taux de faux positifs.
La correction de Holm
Comment utiliser la correction de Holm (notez ce qui arrive aux \(p\)-valeurs):
p1 p2 p3 p4 p5
0.88 0.59 0.43 0.30 0.27 p1 p2 p3 p4 p5
1 1 1 1 1 ## Pour montrer ce qui se passe avec des p-valeurs "significatives"
theps_new <- sort(c(theps, newlowp = .01))
p.adjust(theps_new, method = "holm")newlowp p5 p4 p3 p2 p1
0.06 1.00 1.00 1.00 1.00 1.00 Approches pour tester des hypothèses avec plusieurs bras
Le même genre de problème peut arriver lorsque la question porte sur l’effet différentiel d’un traitement multi-bras.
Avec 5 bras, “l’effet du bras 1” pourrait signifier beaucoup de choses différentes : “Est-ce que les résultats potentiels moyens sont plus grands pour le bras 1 par rapport au bras 2 ?”, “Les résultats potentiels sont-ils plus grands pour le bras 1 comparé à tous les autres ?”
Si nous nous concentrons uniquement sur les comparaisons par paires de bras, nous pourrions avoir \(((5 \times 5) - 5)/2 = 10\) tests uniques !
Tests d’hypothèses multiples : bras de traitement multiples
Voici quelques résultats potentiels et observés quand T
prend plusieurs valeurs.
ID T Y_T_2 Y_T_3 Y_T_4 Y_T_5 Y
1 001 3 0.366 0.546 -0.626 -0.125 0.546
2 002 3 0.931 -2.233 1.309 1.078 -2.233
3 003 4 -1.907 0.288 -0.133 -1.261 -0.133
4 004 5 0.052 0.544 -1.608 -0.452 -0.452
5 005 2 -0.848 -1.192 -1.308 -1.027 -0.848
6 006 3 -0.368 -0.018 -0.045 0.068 -0.018Tests d’hypothèses multiples : bras de traitement multiples
Voici les 10 tests par paire avec et sans ajustement pour les tests multiples. Remarquez comment un résultat “significatif” (\(p=0,01\)) change avec l’ajustement.
Comparison Stat p.value p.adjust
1 1 - 2 = 0 1.435 0.231 1.0000
2 1 - 3 = 0 0.8931 0.3447 1.0000
3 1 - 4 = 0 6.404 0.01139 0.1139
4 1 - 5 = 0 0.8216 0.3647 1.0000
5 2 - 3 = 0 0.05882 0.8084 1.0000
6 2 - 4 = 0 2.641 0.1041 0.7287
7 2 - 5 = 0 0.0437 0.8344 1.0000
8 3 - 4 = 0 3.232 0.07222 0.6500
9 3 - 5 = 0 0.0003464 0.9852 1.0000
10 4 - 5 = 0 2.899 0.08861 0.7089Tests d’hypothèses multiples : bras de traitement multiples
Nous illustrons quatre approches différentes :
- faire tous les tests par paire et choisir le meilleur (une mauvaise idée) ;
- faire tous les tests par paire et choisir le meilleur après avoir ajusté les p-valeurs pour les tests multiples (une bonne idée mais avec une très faible puissance statistique) ;
- tester l’hypothèse d’absence de relation pour chaque bras (un test omnibus) et le résultat (une bonne idée) ;
- choisissez un bras sur lequel vous concentrer à l’avance (une bonne idée).
| estimator | fwer |
|---|---|
| Choix du meilleur test de paire | 0.238 |
| Choix du meilleur test de paire après ajustement | 0.028 |
| T-test T1 vs. tous | 0.018 |
| Test d’ensemble | 0.034 |
Résumé
Utiliser plusieurs résultats ou plusieurs traitements (ou plusieurs modérateurs/interactions) peut causer des problèmes de test.
La procédure pour faire les tests d’hypothèses et intervalles de confiance peut comporter des erreurs. Normalement on contrôle le taux d’erreur dans un seul test (ou un seul intervalle de confiance). Mais utiliser plusieurs tests nécessite plus d’effort pour s’assurer que le taux d’erreur est sous contrôle.
La perte de puissance statistique induite par les approches d’ajustement nous incite à réfléchir aux questions que nous voulons poser sur les données. Par exemple, si nous voulons savoir si le traitement a eu un quelconque effet, alors un test conjoint ou un test omnibus de résultats multiples augmentera notre puissance statistique sans nécessiter d’ajustement.
Comment faire cela en R : COIN