La puissance statistique
Mettre votre nom
02-03-2022
Qu’est-ce que la puissance statistique ?
Qu’est-ce que la puissance statistique ?
Nous voulons séparer le signal du bruit.
Puissance statistique = probabilité de rejeter l’hypothèse nulle, compte tenu d’un effet réel \(\ne\) 0.
En d’autres termes, c’est la capacité à détecter un effet étant donné qu’il existe.
Formellement : (1 - Type II) taux d’erreur.
Ainsi, la puissance statistique \(\in\) (0, 1).
Seuils standard : 0,8 ou 0,9.
Point de départ pour l’analyse de puissance
L’analyse de puissance est quelque chose que nous faisons avant de mener une étude pour aider à :
déterminer l’échantillon dont vous avez besoin pour détecter une taille d’effet donnée.
déterminer une différence détectable minimale compte tenu d’une taille d’échantillon définie.
décider si vous souhaitez mener une étude.
Il est difficile d’apprendre d’un résultat nul sous-alimenté.
- Y a-t-il eu un effet, mais nous n’avons pas pu le détecter ? N’y a-t-il eu aucun effet ? Impossible à dire.
La puissance statistique
Disons qu’il y a vraiment un effet de traitement et que vous exécutez votre expérience plusieurs fois. À quelle fréquence obtiendrez-vous un résultat statistiquement significatif ?
Quelques conjectures pour répondre à cette question.
Quelle est l’ampleur de l’effet de votre traitement ?
Combien d’unités sont traitées, mesurées ?
Quelle quantité de bruit y a-t-il dans la mesure de votre résultat ?
Approches pour calculer la puissance statistique
Calcul analytique
Simulation
Outils de calcul de puissance statistique
Interactifs
Packages R
DeclareDesign, voir aussi https://declaredesign.org/
Calcul analytique de puissance
Calcul analytique de puissance
Formule: \[\begin{align*} \text{Puissance} &= \Phi\left(\frac{|\tau| \sqrt{N}}{2\sigma}- \Phi^{-1}(1- \frac{\alpha}{2})\right) \end{align*}\]
Composants:
- \(\phi\) : la fonction de répartition de la loi normale (strictement croissante)
- \(\tau\) : la taille de l’effet
- \(N\) : la taille de l’échantillon
- \(\sigma\) : l’écart type du résultat
- \(\alpha\) : le niveau de signification (typiquement 0,05)
Exemple : calcul analytique de puissance
# Puissance statistique pour une étude avec 80 observations
# et un effet de taille de 0,25
library(pwr)
pwr.t.test(
n = 40, d = 0.25, sig.level = 0.05,
power = NULL, type = c(
"two.sample",
"one.sample", "paired"
)
)
Two-sample t test power calculation
n = 40
d = 0.25
sig.level = 0.05
power = 0.1972
alternative = two.sided
NOTE: n is number in *each* groupLimites du calcul analytique de puissance
Dérivé uniquement pour certaines statistiques de test (différence des moyennes)
Fait des hypothèses spécifiques sur le processus de génération de données
Incompatible avec des conceptions plus complexes
Calcul de puissance par simulation
Calcul de puissance par simulation
Créer un ensemble de données et simuler la conception de recherche.
Des hypothèses sont nécessaires pour les études de simulation, mais vous faites les vôtres.
Pour l’approche DeclareDesign, voir https://declaredesign.org/
Étapes
Définir l’échantillon et la fonction des résultats potentiels.
Définir la procédure d’assignation du traitement.
Créer des données.
Assigner un traitement, puis estimer l’effet.
Répéter de nombreuses fois.
Exemples
Randomisation complète
Avec covariables
Avec une randomisation par grappe
Exemple : Calcul de puissance par simulation pour une randomisation complète
# install.packages("randomizr")
library(randomizr)
library(estimatr)
## Y0 est fixe dans la plupart des expériences sur le terrain.
## Nous ne le générons donc qu'une seule fois:
make_Y0 <- function(N) {
rnorm(n = N)
}
repeat_experiment_and_test <- function(N, Y0, tau) {
Y1 <- Y0 + tau
Z <- complete_ra(N = N)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z)
pval <- estimator$p.value[2]
return(pval)
}Exemple : Calcul de puissance par simulation pour une randomisation complète
power_sim <- function(N, tau, sims) {
Y0 <- make_Y0(N)
pvals <- replicate(
n = sims,
repeat_experiment_and_test(N = N, Y0 = Y0, tau = tau)
)
pow <- sum(pvals < .05) / sims
return(pow)
}
set.seed(12345)
power_sim(N = 80, tau = .25, sims = 100)[1] 0.15[1] 0.21Exemple : Avec DeclareDesign
library(DeclareDesign)
library(tidyverse)
P0 <- declare_population(N, u0 = rnorm(N))
# declarer Y(Z=1) et Y(Z=0)
O0 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
# assigner m unités au traitement
A0 <- declare_assignment(Z = conduct_ra(N = N, m = round(N / 2)))
# le paramètre est la différence moyenne entre Y(Z=1) et Y(Z=0)
estimand_ate <- declare_inquiry(ATE = mean(Y_Z_1 - Y_Z_0))
R0 <- declare_reveal(Y, Z)
design0_base <- P0 + A0 + O0 + R0
## Par exemple:
design0_N100_tau25 <- redesign(design0_base, N = 100, tau = .25)
dat0_N100_tau25 <- draw_data(design0_N100_tau25)
head(dat0_N100_tau25) ID u0 Z Y_Z_0 Y_Z_1 Y
1 001 -0.2060 0 4.794 5.044 4.794
2 002 -0.5875 0 4.413 4.663 4.413
3 003 -0.2908 1 4.709 4.959 4.959
4 004 -2.5649 0 2.435 2.685 2.435
5 005 -1.8967 0 3.103 3.353 3.103
6 006 -1.6401 1 3.360 3.610 3.610[1] 0.25[1] 0.5569(Intercept) Z
4.8458 0.5569 E0 <- declare_estimator(Y ~ Z,
model = lm_robust, label = "test-t 1",
inquiry = "ATE"
)
t_test <- function(data) {
test <- with(data, t.test(x = Y[Z == 1], y = Y[Z == 0]))
data.frame(statistic = test$statistic, p.value = test$p.value)
}
T0 <- declare_test(handler = label_test(t_test), label = "test-t 2")
design0_plus_tests <- design0_base + E0 + T0
design0_N100_tau25_plus <- redesign(design0_plus_tests, N = 100, tau = .25)
## Répète seulement l'assignation aléatoire, pas la création de Y0.
## Ignorer le warning
names(design0_N100_tau25_plus)[1] "P0" "A0" "O0" "R0" "test-t 1" "test-t 2"design0_N100_tau25_sims <- simulate_design(design0_N100_tau25_plus,
sims = c(1, 100, 1, 1, 1, 1)
) # Répète seulement l'assignation aléatoireWarning: We recommend you choose a higher number of simulations than 1 for the top level of simulation.# design0_N100_tau25_sims a 200 lignes
# = 2 tests * 100 assignations aleatoires
# regardons les 6 premières lignes
head(design0_N100_tau25_sims) design N tau sim_ID estimator term estimate std.error statistic p.value conf.low conf.high df outcome inquiry
1 design0_N100_tau25_plus 100 0.25 1 test-t 1 Z 0.1108 0.2150 0.5153 0.60752 -0.3158 0.5374 98 Y ATE
2 design0_N100_tau25_plus 100 0.25 1 test-t 2 <NA> NA NA 0.5153 0.60754 NA NA NA <NA> <NA>
3 design0_N100_tau25_plus 100 0.25 2 test-t 1 Z 0.2458 0.2154 1.1411 0.25661 -0.1817 0.6733 98 Y ATE
4 design0_N100_tau25_plus 100 0.25 2 test-t 2 <NA> NA NA 1.1411 0.25662 NA NA NA <NA> <NA>
5 design0_N100_tau25_plus 100 0.25 3 test-t 1 Z 0.5463 0.2133 2.5608 0.01197 0.1229 0.9697 98 Y ATE
6 design0_N100_tau25_plus 100 0.25 3 test-t 2 <NA> NA NA 2.5608 0.01203 NA NA NA <NA> <NA>
step_1_draw step_2_draw
1 1 1
2 1 1
3 1 2
4 1 2
5 1 3
6 1 3# pour chaque estimateur,
# puissance = proportion de simulations avec une p-valeur < 0,05
design0_N100_tau25_sims %>%
group_by(estimator) %>%
summarize(pow = mean(p.value < .05), .groups = "drop")# A tibble: 2 × 2
estimator pow
<chr> <dbl>
1 test-t 1 0.2
2 test-t 2 0.2Puissance statistique avec ajustement de covariable
Ajustement de covariable et puissance statistique
L’ajustement de covariable peut améliorer la puissance statistique car il atténue la variation du résultat.
S’il est pronostique, l’ajustement de covariable peut réduire considérablement la variance. Une variance plus faible signifie une puissance plus élevée.
S’il est non pronostique, les gains de puissance sont minimes.
Toutes les covariables doivent être pré-traitement. N’abandonnez pas d’observations pour cause de données manquantes.
- Voir le module sur les menaces à la validité interne et les 10 choses à savoir sur l’ajustement de covariable.
Observez le biais de Freedman tandis que le nombre d’observations n diminue et que le nombre de covariables K augmente.
Découpage par bloc
Découper par bloc : assignez de manière aléatoire un traitement au sein des blocs
Ajustement de covariable “ex-ante”
Une précision/efficacité plus élevée implique plus de puissance statistique
Réduire le “biais conditionnel” : association entre l’assignation du traitement et les résultats potentiels
L’avantage des blocs sur l’ajustement de covariable est plus clair dans les petites expériences
Exemple : Calcul de puissance par simulation avec une covariable
## Y0 est fixe dans la plupart des expériences sur le terrain.
## Nous ne le générons donc qu'une seule fois:
make_Y0_cov <- function(N) {
u0 <- rnorm(n = N)
x <- rpois(n = N, lambda = 2)
Y0 <- .5 * sd(u0) * x + u0
return(data.frame(Y0 = Y0, x = x))
}
## X prédit modérément Y0.
test_dat <- make_Y0_cov(100)
test_lm <- lm_robust(Y0 ~ x, data = test_dat)
summary(test_lm)
Call:
lm_robust(formula = Y0 ~ x, data = test_dat)
Standard error type: HC2
Coefficients:
Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
(Intercept) 0.11 0.1880 0.585 0.559753653 -0.263 0.483 98
x 0.44 0.0814 5.413 0.000000441 0.279 0.602 98
Multiple R-squared: 0.231 , Adjusted R-squared: 0.223
F-statistic: 29.3 on 1 and 98 DF, p-value: 0.000000441## maintenant mettre en place la simulation
repeat_experiment_and_test_cov <- function(N, tau, Y0, x) {
Y1 <- Y0 + tau
Z <- complete_ra(N = N)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z + x, data = data.frame(Y0, Z, x))
pval <- estimator$p.value[2]
return(pval)
}
## créer les données une fois
## assigner de manière aléatoire le traitement sims fois
## rapporte quelle proportion renvoie une valeur p < 0,05
power_sim_cov <- function(N, tau, sims) {
dat <- make_Y0_cov(N)
pvals <- replicate(n = sims, repeat_experiment_and_test_cov(
N = N,
tau = tau, Y0 = dat$Y0, x = dat$x
))
pow <- sum(pvals < .05) / sims
return(pow)
}Exemple : Calcul de puissance par simulation avec une covariable IV
[1] 0.13[1] 0.19Puissance statistique pour la randomisation par grappe
Puissance statistique et conception par grappe
Voir le module sur la randomisation.
Etant donné un \(N\) fixe, une conception par grappe est légèrement moins puissante qu’une conception sans grappe.
- La différence est souvent substantielle.
Il faut estimer correctement la variance :
- erreur type robuste pour grappe (robust clustered standard error, RCSE)
- Inférence de randomisation
Pour augmenter la puissance :
- Mieux vaut augmenter le nombre de grappes que le nombre d’unités par grappe.
- Dans quelle mesure les grappes réduisent la puissance statistique dépend de manière critique de la corrélation intra-grappe (intra-cluster correlation, ICC) (i.e. le rapport de la variance au sein des grappes à la variance totale).
La conception par grappe dans la recherche observationelle
Souvent négligé, conduisant à (peut-être) une incertitude extrêmement sous-estimée.
Inférence fréquentiste basée sur le ratio \(\hat{\beta}/\hat{se}\)
Si nous sous-estimons \(\hat{se}\), nous sommes beaucoup plus susceptibles de rejeter \(H_0\). (Le taux d’erreur de type I est trop élevé.)
De nombreuses conceptions d’observation sont beaucoup moins puissantes qu’on ne le pense.
Exemple : Puissance statistique basée sur la simulation pour la randomisation par grappe
## Y0 est fixe dans la plupart des expériences sur le terrain.
## Nous ne le générons donc qu'une seule fois:
make_Y0_clus <- function(n_indivs, n_clus) {
# n_indivs est le nombre de personnes par grappe
# n_clus est le nombre de grappes
clus_id <- gl(n_clus, n_indivs)
N <- n_clus * n_indivs
u0 <- fabricatr::draw_normal_icc(N = N, clusters = clus_id, ICC = .1)
Y0 <- u0
return(data.frame(Y0 = Y0, clus_id = clus_id))
}
test_dat <- make_Y0_clus(n_indivs = 10, n_clus = 100)
# confirmer que cela produit des données avec 10 dans chacune des 100 grappes
table(test_dat$clus_id)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
100
10 [1] 0.09655repeat_experiment_and_test_clus <- function(N, tau, Y0, clus_id) {
Y1 <- Y0 + tau
# ici, nous randomisons Z au niveau de la grappe
Z <- cluster_ra(clusters = clus_id)
Yobs <- Z * Y1 + (1 - Z) * Y0
estimator <- lm_robust(Yobs ~ Z,
clusters = clus_id,
data = data.frame(Y0, Z, clus_id), se_type = "CR2"
)
pval <- estimator$p.value[2]
return(pval)
}
power_sim_clus <- function(n_indivs, n_clus, tau, sims) {
dat <- make_Y0_clus(n_indivs, n_clus)
N <- n_indivs * n_clus
# randomiser le traitement sims fois
pvals <- replicate(
n = sims,
repeat_experiment_and_test_clus(
N = N, tau = tau,
Y0 = dat$Y0, clus_id = dat$clus_id
)
)
pow <- sum(pvals < .05) / sims
return(pow)
}[1] 0.66[1] 0.68Exemple : Puissance statistique basée sur la simulation pour la randomisation par grappe (DeclareDesign)
P1 <- declare_population(
N = n_clus * n_indivs,
clusters = gl(n_clus, n_indivs),
u0 = draw_normal_icc(N = N, clusters = clusters, ICC = .2)
)
O1 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
A1 <- declare_assignment(Z = conduct_ra(N = N, clusters = clusters))
estimand_ate <- declare_inquiry(ATE = mean(Y_Z_1 - Y_Z_0))
R1 <- declare_reveal(Y, Z)
design1_base <- P1 + A1 + O1 + R1 + estimand_ate
## Par exemple:
design1_test <- redesign(design1_base, n_clus = 10, n_indivs = 100, tau = .25)
test_d1 <- draw_data(design1_test)
# confirmer que tous les individus d'un groupe
# ont la même assignation de traitement
with(test_d1, table(Z, clusters)) clusters
Z 1 2 3 4 5 6 7 8 9 10
0 100 0 100 100 100 0 0 100 0 0
1 0 100 0 0 0 100 100 0 100 100# les trois estimateurs diffèrent par se_type:
E1a <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "CR2", label = "test-t CR2 (robuste pour grappe)",
inquiry = "ATE"
)
E1b <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "CR0", label = "test-t CR0 (robuste pour grappe)",
inquiry = "ATE"
)
E1c <- declare_estimator(Y ~ Z,
model = lm_robust, clusters = clusters,
se_type = "stata", label = "test-t RCSE en stata",
inquiry = "ATE"
)
design1_plus <- design1_base + E1a + E1b + E1c
design1_plus_tosim <- redesign(design1_plus, n_clus = 10, n_indivs = 100, tau = .25)## Répéter seulement l'assignation aléatoire, pas la création de Y0.
## Ignorer le warning
## Nous voudrions plus de simulations en pratique.
set.seed(12355)
design1_sims <- simulate_design(design1_plus_tosim,
sims = c(1, 1000, rep(1, length(design1_plus_tosim) - 2))
)Warning: We recommend you choose a higher number of simulations than 1 for the top level of simulation.design1_sims %>%
group_by(estimator) %>%
summarize(
puissance = mean(p.value < .05),
couverture = mean(estimand <= conf.high & estimand >= conf.low),
.groups = "drop"
)# A tibble: 3 × 3
estimator puissance couverture
<chr> <dbl> <dbl>
1 test-t CR0 (robuste pour grappe) 0.155 0.911
2 test-t CR2 (robuste pour grappe) 0.105 0.936
3 test-t RCSE en stata 0.131 0.918library(DesignLibrary)
## Cela peut être plus simple que ce qui précède :
d1 <- block_cluster_two_arm_designer(
N_blocks = 1,
N_clusters_in_block = 10,
N_i_in_cluster = 100,
sd_block = 0,
sd_cluster = .3,
ate = .25
)
d1_plus <- d1 + E1b + E1c
d1_sims <- simulate_design(d1_plus, sims = c(1, 1, 1000, 1, 1, 1, 1, 1))d1_sims %>%
group_by(estimator) %>%
summarize(
puissance = mean(p.value < .05),
couverture = mean(estimand <= conf.high & estimand >= conf.low),
.groups = "drop"
)# A tibble: 3 × 3
estimator puissance couverture
<chr> <dbl> <dbl>
1 estimator 0.143 0.941
2 test-t CR0 (robuste pour grappe) 0.209 0.914
3 test-t RCSE en stata 0.194 0.925Statique comparative
Statique comparative
- La puissance
- augmente avec \(N\)
- augmente avec \(|\tau|\)
- diminue avec \(\sigma\)
Puissance par taille d’échantillon
some_ns <- seq(10, 800, by = 10)
pow_by_n <- sapply(some_ns, function(then) {
pwr.t.test(n = then, d = 0.25, sig.level = 0.05)$power
})
plot(some_ns, pow_by_n,
xlab = "Taille d'échantillon",
ylab = "Puissance"
)
abline(h = .8)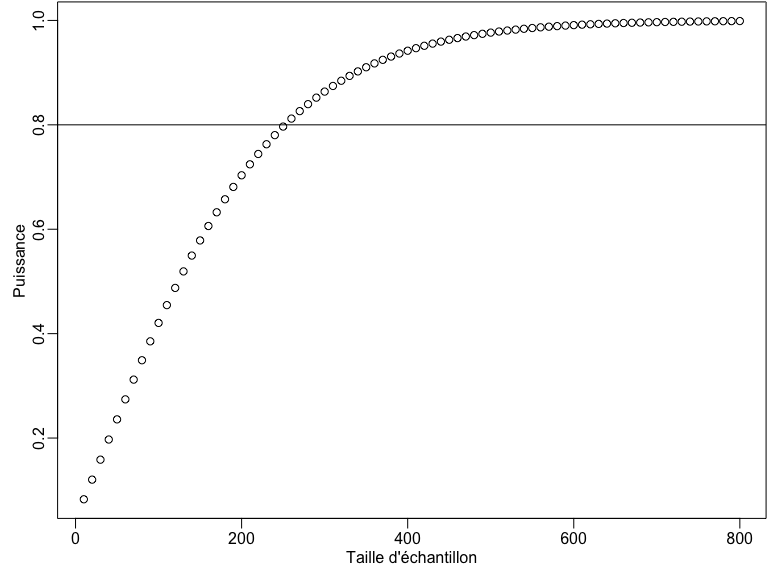
Puissance par taille d’effet de traitement
some_taus <- seq(0, 1, by = .05)
pow_by_tau <- sapply(some_taus, function(thetau) {
pwr.t.test(n = 200, d = thetau, sig.level = 0.05)$power
})
plot(some_taus, pow_by_tau,
xlab = "Effet moyen du traitement (standardisé)",
ylab = "Puissance"
)
abline(h = .8)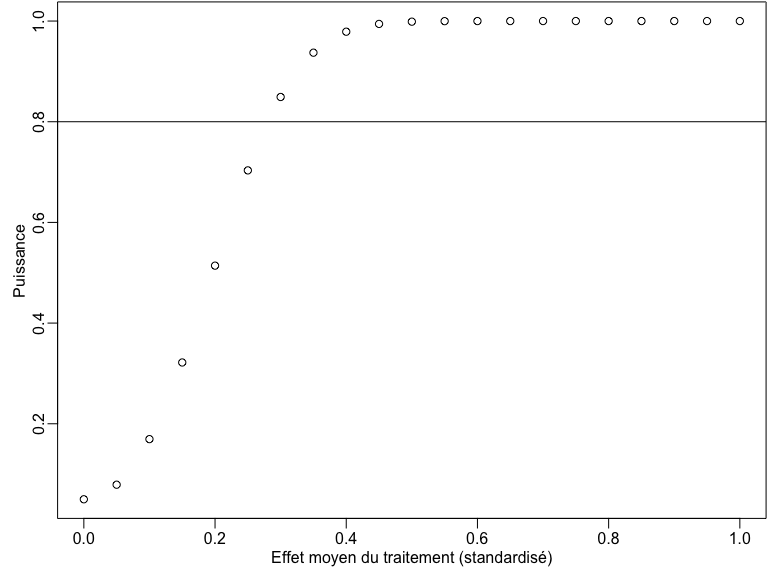
La calculateur de puissance EGAP
À essayer sur https://egap.shinyapps.io/power-app/
Pour les conceptions de randomisation par grappe, essayez d’ajuster:
- Nombre de grappes
- Nombre d’unités par grappe
- Corrélation intra-grappe
- Effet de traitement
Commentaires
Connaissez votre variable de résultat.
Quels effets pouvez-vous réellement attendre de votre traitement ?
Quelle est la plage de variation plausible de la variable de résultat ?
- Une conception peut ne pas être puissante si le mouvement possible est limité pour la variable de résultat.
Conclusion : comment améliorer votre puissance
Augmenter \(N\)
- En cas de grappe, augmenter le nombre de grappes si possible
Renforcer le traitement
Améliorer la précision
Ajustement de covariable
Découpage par bloc
Meilleure mesure de la variable de résultat